Георг Гегель - Наука логики. Том I. Объективная логика

Urteil (суждение) буквально перво-часть, urteilen (судить) — перво-делить. — Перев .

Я напомню, что в настоящем сочинении я потому так часто принимаю во внимание кантовскую философию (это некоторым читателям может казаться нелишним), что, как бы ни смотрели другие, а также и мы в настоящем сочинении на детали, на отдельные ее черты, равно как и на разработку особенных частей ее, она все же составляет основу и исходный пункт новейшей немецкой философии; и эта ее заслуга остается неумаленной тем, что в ней подлежит критике. Ее приходится часто принимать во внимание в объективной логике также и потому, что она подвергает тщательному рассмотрению важные, более определенные стороны логического, между тем как позднейшие изложения философии, напротив, уделяли ему мало внимания и часто только высказывали по отношению к нему грубое, но не оставшееся без возмездия, презрение. Философское учение, пользующееся у нас наиболее широким распространением, не идет дальше кантовских выводов, согласно которым разум не способен познать никакого истинного содержания и в отношении абсолютной истины следует отсылать к вере. Но это философствование непосредственно начинает тем, что у Канта представляет собою только вывод, и этим наперед отрезывает предшествующие соображения, из которых вытекает указанный вывод и которые именно и представляют собою философское познание. Кантовская философия служит, таким образом, подушкой для лености мысли, успокаивающейся на том, что все уже доказано и порешено. За познанием и определенным содержанием мышления, которых не найти в таком бесплодном и сухом успокоении, следует, поэтому, обращаться к указанным предшествующим соображениям.

Если выражение « объективирующее делание» «я» может напомнить о других продуктах духа, например, о продуктах фантазии , то следует заметить, что речь идет об определении предмета, поскольку его содержательные моменты не принадлежат области чувства и созерцания . Такой предмет есть некая мысль , и определить его означает частью впервые его продуцировать, частью же, поскольку он есть нечто предположенное, иметь о нем дальнейшие мысли, мыслительно развивать его далее.

«Kants Kritik der r. Vern.», 2-te Aufl., 628 (19).

Немецкое слово Bestimmung означает как определение, так и назначение. — Перев .

Идеальное имеет дальнейшее, более определенное значение (прекрасного и того, что ведет к последнему), чем идеализованное ; первому здесь еще не место; поэтому мы здесь употребляем выражение: « идеализованное ». В отношении к реальности это различие в словоупотреблении не имеет место; «das Reelle» и «das Reale» употребляются приблизительно в одном и том же значении. Выяснение оттенков этих двух выражений в их отличии друг от друга не представляет интереса.

К излишеству в самом способе доказательства присоединяется здесь еще излишество слов: «Так как у последних (именно, у субстанций) сложность есть лишь случайное отношение субстанций ».

Grad по-немецки степень интенсивности, градус. В большинстве случаев мы предпочли передавать «Grad» не через «степень», а через «градус», чтобы избежать смешения с «Potenz» (математическая степень), хотя «градус», может быть, несколько затушевывает качественный характер интенсивной величины. — Перев .

Anzahl; перевод через «численность» дан Лениным, хотя и предположительно и как один из возможных переводов (см. «Ленинский сборник» IX, стр. 82). Дебольский переводит — «определенное число»; в томе I Собрания сочинений Гегеля. — «определенное множество». — Перев .

В примечании к тезису первой космологической антиномии в «Критике чистого разума».

Обе точки зрения весьма просто сопоставлены у Лагранжа при применении теории функций в механике, в главе о прямолинейном движении (Théorie des fonct. 3-me р., ch. I, art. IV). Если рассматривать пройденное пространство как функцию протекшего времени, то получается уравнение , которое, разложенное как 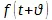, дает 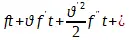и т. д. Следовательно, пространство, пройденное в данное время, изображается формулой и т. д. Движение, посредством которого проходится это пространство, говорят нам, составлено , следовательно (т. е. вследствие того, что аналитическое разложение в ряд дает много и притом бесконечно много членов) — из различных частичных движений, соответствующие времени пространства которых суть 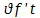, , 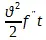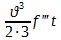и т. д. Первое частичное движение есть в известном нам движении формально-равномерное движение со скоростью 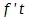, второе равномерно ускоренное, зависящее от силы ускорения, пропорциональной 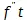. «А так как прочие члены не относятся ни к какому простому известному движению, то нет надобности принимать их в отдельности во внимание , и мы покажем, что от них можно абстрагироваться при определении движения в начале момента времени». Это и показывается, но, конечно, только путем сравнения вышеуказанного ряда, члены которого все должны были служить для определения величины пространства, пройденного в данное время, с данным в § 3 для падения тел уравнением 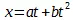, в котором имеются только эти два члена. Но это уравнение само получило этот вид лишь благодаря предположению объяснения , даваемого членам, возникающим посредством аналитического разложения в ряд , это предположение заключается в том, что равномерно ускоренное движение составлено из формально равномерного движения, совершающегося с достигнутой в предыдущую часть времени скоростью, и некоторого прибавка ( a в уравнении 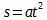), т. е. эмпирического коэфициента, приписываемого силе тяжести, а ведь это есть такое различение, которое отнюдь не имеет существования или основания в природе вещей, но есть лишь ошибочно получившее характер физического положения выражение того, что получается при принятии некоторой определенной аналитической трактовки.