Моррис Коэн - Введение в логику и научный метод

«Да, – отвечаете вы, – но какова польза от часов, которые точно показывают время два раза в день, если я не знаю, когда именно это время наступает?»

Ну почему. Предположим, часы указывают на 8 часов. Разве вы не знаете, что если сейчас 8 часов, то это правильное время? Следовательно, когда наступает 8 часов, то ваши часы верно на него показывают.

«Да, это я понимаю», – отвечаете вы.

Отлично, в таком случае вы противоречите себе дважды: теперь выпутайтесь из этой сложности и постарайтесь при этом больше себе не противоречить.

Далее вы можете спросить: «Откуда мне знать, когда наступает 8 часов? Мои часы мне этого не скажут». Имейте терпение. Вы ведь знаете, что когда наступает 8 часов, то ваши часы верно показывают время? Очень хорошо. В таком случае вашим правилом будет следующее: внимательно следите за своими часами, и каждый раз, когда они будут верно показывать время, будет 8 часов. «Но…» – возражаете вы. Хорошо, достаточно. Чем больше вы спорите, тем дальше вы уходите от вопроса, поэтому не лучше ли прекратить? (Льюис Кэрролл)

Для дальнейшего изучения:

Venn J. Empirical Logic. Chap. X.

Keynes J. N. Formal Logic. 4 ed. Appendix C. Chap. V.

1. Укажите, какое отношение имеет место в каждом из следующих примеров: транзитивное, интранзитивное, симметричное, асимметричное, одно‑однозначное, одно‑многозначное или много‑многозначное.

a. Он самый низкорослый в армии.

b. Джозеф имел тех же родителей, что и Бенжамин.

c. Адам является предком всех нас.

d. Нетерпение не является свойством хорошего преподавателя.

e. Смит является соседом Джонса.

f. Россия потерпела поражение от Японии.

g. Ромео – возлюбленный Джульетты.

h. Агент по продаже билетов знаком со многими знаменитостями.

i. Браун – наемный работник Джексона.

2. Обсудите содержание данного отрывка:

«Крайне ошибочным трюизмом, считающимся прописной истиной и повторяемым в речах высокопоставленных людей, является утверждение о том, что мы должны вырабатывать привычку думать о том, что мы делаем. На самом же деле, происходит обратное. Цивилизация развивается, увеличивая количество важных операций, выполнять которые мы можем, не думая. Мысленные операции подобны кавалерийским расчетам при сражении – их число крайне ограничено, им требуются свежие лошади и задействоваться они должны исключительно в решающих ситуациях» [133] .

3. Сформулируйте следующие выражения словами и упростите их:

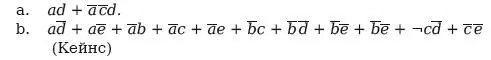
4. Покажите, что:

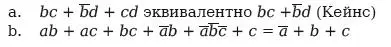
5. Приведите суждения, противоречащие данным:

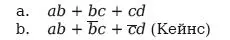
6. Приведите суждения, противоречащие данным:

a. Цветущие растения являются либо эндогенными, либо экзогенными, но ни то и другое одновременно.

b. Цветущие растения являются васкулярными, а также являются либо эндогенными, либо экзогенными, но ни то и другое одновременно.

7. Назовите некоторые сложности использования разговорного языка для отдельных целей науки.

8. Проверьте по толковому словарю изменение в значении таких слов, как «вид», «рукопись», «часы», «род», «доктор».

9. Что означает класс?

10. Что означает логическая сумма двух классов? Логическое произведение двух классов?

11. Что означает утверждение, что один из двух классов включен в другой?

12. Что такое нуль-класс и каковы отношения между этим классом и любым другим классом?

13. Выразите нижеприведенные суждения в символической форме:

a. Только настойчивые добиваются успеха.

b. Некоторые профессора не являются седыми.

c. Никто, кроме молодых, не способен на героизм.

d. Все книги по логике содержат опечатки.

e. Ни один спортсмен не живет долго.

14. Докажите в символической форме:

a. Все а суть Ь; следовательно, все не-b суть не-а.

b. Ни один а не является Ь; следовательно, все а являются не-Ь.

c. Некоторые а суть Ь; следовательно, некоторые Ь суть а.

d. Некоторые а не суть Ь; следовательно, некоторые не-Ь не суть не-а.

15. Выразите в символической форме:

a. Если р имплицирует q, a q имплицирует г, то р имплицирует г.

b. Если р и q имплицируют г, то р и не-г имплицируют н e-q.

c. Если р или q имплицирует г, то либо р имплицирует г, либо q имплицирует г.

Для дальнейшего изучения:

Couturat L. Algebra of Logic.

Whitehead A. N. Universal Algebra, Bk. I, Chap. I and Book II. Lewis С. I., Langford. Symbolic Logic.

Eaton R. M. Symbolism and Truth. Chap. VII.

О природе символов:

Johnson W. E. Logic, Part II. Chap. III.

Whitehead A. N. An Introduction to Mathematics. Chap. V.

Eaton R. M. Symbolism and Truth. Chap. II.

1. Установите то, что нижеследующие постулаты являются непротиворечивыми. Также покажите, что они независимы друг от друга.

Постулат 1. Если а и Ь – различные элементы класса К, и < – некоторое отношение, то а < b или Ь < а.

Постулат 2. Если а < Ь, то а и Ь различны.

Постулат 3. Если а < Ь, то Ь < с, тогда а < с [134] .

2. Покажите, что набор операций (сложения, умножения, деления и вычитания) над целыми числами является изоморфным набору операций над дробями.

3. Обсудите отношение алгебры к аналитической геометрии в свете вопроса об изоморфизме.

4. Докажите, что аристотелевский принцип dictum de omni et nullo для категорического силлогизма является эквивалентным пяти аксиомам обоснованности, сформулированным в § 3 главы IV.

5. Покажите, что аксиома I для категорического силлогизма (средний термин должен быть распределен хотя бы единожды) является эквивалентной аксиоме 2 (ни один термин не может быть распределенным в заключении, если он не распределен в посылках).

6. «Напишите на одной карточке любое нечетное число, например 35, а на другой – любое четное, например 46. Попросите, чтобы кто-то дал одну карточку А, а другую – Б, но при этом так, чтобы вы не знали, у кого из них какая карточка. Ваша задача сообщить А о том, какое число написано у него на карточке. Скажите, чтобы А умножил свое число на любое четное, а В свое – на любое нечетное. Попросите А и В сложить получившиеся у них в результате умножения числа и назвать вам получившуюся сумму. Если сумма – четная, то у А изначально на карточке было нечетное число, если сумма – нечетная, то у А изначально было четное число» [135] . Докажите, что данный результат будет всегда сохраняться.

7. Покажите, что невозможно разложить целое число на множители, являющиеся простыми числами, более чем одним способом.

8. Что такое аксиома?

9. Что имеется в виду, когда утверждается, что суждение является самоочевидным?