Josep Carrera - Трехмерный мир. Евклид. Геометрия

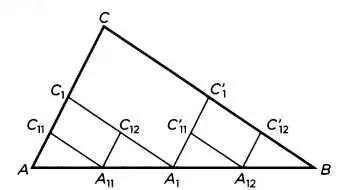
РИС. 3

Евклид открывает книгу XII двумя предложениями, которые устанавливают одну и ту же теорему для правильных многоугольников, вписанных в круг, и для круга.

Книга XII,предложение 1. Подобные многоугольники, вписанные в круги, будут относиться друг к другу как квадраты диаметров этих кругов.

Книга XII,предложение 2. Круги относятся друг к другу как квадраты их диаметров.

Первое предложение является прямым следствием теоремы Фалеса применительно к площадям, поскольку достаточно убедиться, что каждый из центральных треугольников, на которые раскладываются правильные многоугольники, подтверждает теорему Фалеса. Второе можно было бы доказать методом бесконечного ряда, но рассуждения, в которых используется понятие бесконечности, были неприемлемы для древнегреческих ученых (хотя в этом случае это было бы правильно). Евклид мог бы довести до предела предложение 2 книги XII таким образом: если для каждого многоугольника п вида п=2k справедливо соотношение

Р 1 n/d 2 1 =Р 2 n/d 2 2

и в самом крайнем случае Р 1 nравно S 1а Р 2 nравно S 2то есть от многоугольника переходим к кругу и получаем:

S 1/d 2 1= S 2/d 2 2

Ч.Т.Д.

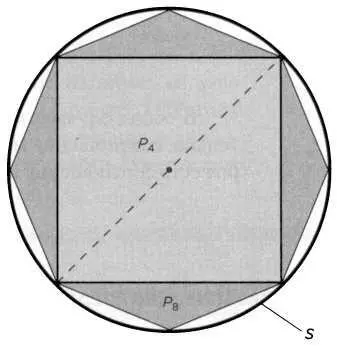
РИС. 4

Правильные многоугольники с 4,8,16,... сторонами все больше заполняют площадь круга.

Отказавшись от предела последовательности, нам остается только применить метод исчерпывания, то есть доказать, что квадрат, вписанный в круг, покрывает больше половины его площади. Если мы добавим треугольники, чтобы получить из квадрата восьмиугольник, получится больше половины площади, оставшейся после того, как мы уберем треугольник, и так далее. В какой-то момент вписанная в круг S многосторонняя фигура Р2k заполнит его так, что оставшееся пространство будет меньше любой другой предыдущей фигуры (см. рисунок 4).

Обратим внимание, что аналогично сказанному в предыдущей главе касательно сегмента параболы равнобедренный треугольник, который мы добавили к каждой стороне квадрата, чтобы получить восьмиугольник, покрывал более половины сегмента окружности, то есть четверть того, что остается от круга, когда мы убираем вписанный квадрат. Затем мы применили те же самые рассуждения к равнобедренным треугольникам, которые строятся на сторонах правильного восьмиугольника, чтобы получить 16-угольник, и так далее. Каждый раз фигуры покрывают более половины, что и необходимо для применения метода исчерпывания.

Пользуясь этим инструментом, Евклид выдвинул два предположения: соотношение площадей либо больше соотношения квадратов диаметров, либо меньше. Запишем оба случая:

(1) S 1/S 2< d 2 1/d 2 2или (2) S 1/S 2> d 2 1/d 2 2

В обоих случаях мы приходим к противоречию. Следовательно, соотношение между площадями и квадратами диаметров есть соотношение равенства.

В случае когда

S 1/S 2< d 2 1/d 2 2(1)

предположим, что существует такая площадь S < S 2, для которой

S 1/S 2= d 2 1/d 2 2

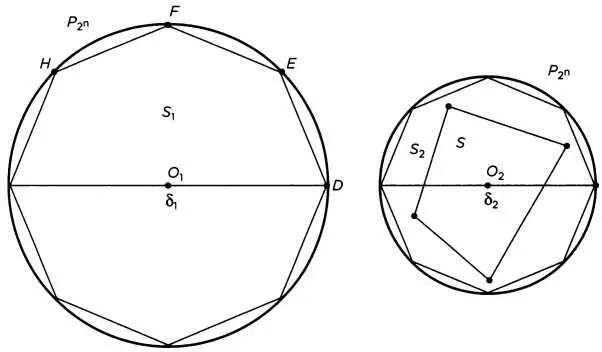
Затем рассмотрим площадь Е = S 2- S. Метод исчерпывания гарантирует, что существует некий многоугольник Р 2, вписанный в S 2, который заполняет его так, что S 2- Р 2< Е = S 2-S. Это приводит к неравенству S < Р 2. Теперь рассмотрим многоугольник Р 2, вписанный в круг (то есть Р 2< S 1, подобный P 2. Из предложения 1 книги XII мы знаем, что

P 1 n/P 2 n= d 2 1/d 2 2,

где n = 2 k. Исходя из общего понятия 1 мы имеем

P 1 n/P 2 n= d 2 1/d 2 2= S 1/S 2,

где S < Р 2и Р 2< S 1, что противоречит определению равенства соотношений (книга V, определение 5). Следовательно, первое допущение (1) неверно. Затем Евклид таким же образом рассматривает второе допущение

S 1/S 2> d 2 1/d 2 2(2)

и приходит к выводу, что оно также неверно. Следовательно, отношение должно быть следующим:

S 1/d 2 1= S 2/d 2 2

Возникают два вопроса. Откуда Евклид знал, что он должен был доказать? Другими словами, почему он взял соотношение именно между площадями и диаметрами? Он неявно использовал метод доведения до предела, который мы рассмотрели выше? Мы не знаем. С другой стороны, для доказательства (1) Евклид предположил существование площади S < S 2, при которой

S 1/S = d 2 1/d 2 2.

Это означает, что при данных площадях S 1, d 2 1, d 2 2он предположил существование «площади S, являющейся четвертой пропорциональной». Однако Евклид доказал ее существование только для трех прямых, а не для трех площадей.

Во второй половине XIX века англичанин Генри Ринд приобрел папирус, датированный примерно 1650 годом до н.э. и названный впоследствии его именем. Этот папирус, в свою очередь, был копией еще более древнего папируса, 1800 года до н.э., и содержал задачи по определению объема цилиндрических силосов для хранения зерна. Его автор, писец Ахмес, хотел узнать площадь круга, лежащего в основании цилиндра, что привело его к определению числа π. В древности его обычно считали равным 3. Однако Ахмес предложил более точное значение π, приблизительно сведя окружность к восьмиугольнику

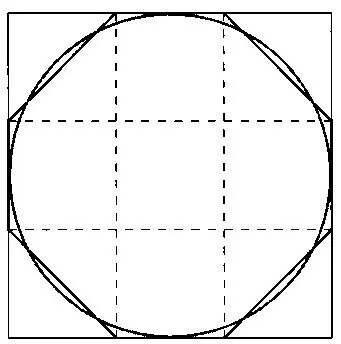
Дан квадрат, состоящий из девяти частей по сторонам. Разделим его на девять квадратов так, что сторона каждого из них будет равна трем этим частям. Уберем четыре прямоугольных треугольника с вершинами, образующимися при проведении диагонали. Площадь получившегося восьмиугольника будет равна

9 ²- 4 x (3 x 3)/2 = 81 -18 = 63

частей в квадрате. Построим площадь круга с диаметром, равным девяти частям и 64 частям в квадрате [то есть 64 — квадрат числа]. Значение к при этом приближении будет равно

π = 64/(9/2)² = (16/9)² = 3.16...

Такое значение π, действительное для всех фигур (то есть при любом значении диаметра d), получается при наложении двух плоских фигур — круга и восьмиугольника. Более тысячи лет спустя Архимед, мудрец из Сиракуз, в своем кратком сочинении «Об измерении круга» изложил два новых результата.

Предложение 1.Отношение L/d, возникающее между длиной окружности L и ее диаметром d, будет равно величине, находящейся между 223/71 и 22/7.

Предложение 2.Площадь круга S равна площади прямоугольного треугольника T, катеты которого равны радиусу r круга и длине L его окружности.