Josep Carrera - Трехмерный мир. Евклид. Геометрия
- Название:Трехмерный мир. Евклид. Геометрия
- Автор:
- Жанр:
- Издательство:ООО “Де Агостини”
- Год:2015
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Josep Carrera - Трехмерный мир. Евклид. Геометрия краткое содержание
Евклид Александрийский — автор одного из самых популярных нехудожественных произведений в истории. Его главное сочинение — «Начала» — было переиздано тысячи раз, на протяжении веков по нему постигали азы математики и геометрии целые поколения ученых. Этот труд состоит из 13 книг и содержит самые важные геометрические и арифметические теории Древней Греции. Не меньшее значение, чем содержание, имеет и вид, в котором Евклид представил научное знание: из аксиом и определений он вывел 465 теорем, построив безупречную логическую структуру, остававшуюся нерушимой вплоть до начала XIX века, когда была создана неевклидова геометрия.
Трехмерный мир. Евклид. Геометрия - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
1. Совершенные числа (четные) оканчиваются на 6 и 8 (верно).
2.Они чередуются (неверно).
3.Существует одно совершенное число на каждый десятичный порядок — среди единиц, десятков, сотен, тысяч и так далее (неверно).
В XVIII веке Эйлер доказал теорему, взаимодополняющую теорему Евклида: каждое совершенное число (четное) имеет вид 2 nх (2 n+1-1), где 2 n+1-1 — простое число. На сегодняшний день все еще существуют нерешенные вопросы относительно совершенных чисел: неизвестно, бесконечен ли их ряд и существуют ли совершенные нечетные числа.
Начнем с последовательности нечетных чисел.
| 3 | 5 | 7 | 9 | 11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 | 31 | 33 | 35 |
| 37 | 39 | 41 | 43 | 45 | 47 | 49 | 51 | 53 | 55 | 57 | 59 | 61 | 63 | 65 | 67 | 69 |
| 71 | 73 | 75 | 77 | 79 | 81 | 83 | 85 | 87 | 89 | 91 | 93 | 95 | 97 | 99 | 101 | 103 |
Начиная с 3 уберем третьи числа через каждые два.
| 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 25 | 29 | 31 | 35 | |||||
| 37 | 41 | 43 | 47 | 49 | 53 | 55 | 59 | 61 | 65 | 67 | ||||||
| 71 | 73 | 77 | 79 | 83 | 85 | 89 | 91 | 95 | 97 | 101 | 103 |
Начиная с 5 уберем пятые числа через каждые пять и получим следующее.
| 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | |||||||
| 37 | 41 | 43 | 47 | 49 | 53 | 59 | 61 | 67 | ||||||||
| 71 | 73 | 77 | 79 | 83 | 89 | 91 | 97 | 101 | 103 |
И так далее. Вот список простых чисел до тысячи.
| 2 | 3 | 5 | 7 | 11 | 13 | 17 | 19 | 23 | 29 | 31 | 37 | 41 | 43 | 47 |
| 53 | 59 | 61 | 67 | 71 | 73 | 79 | 83 | 89 | 97 | 101 | 103 | 107 | 109 | 113 |
| 127 | 131 | 137 | 139 | 149 | 151 | 157 | 163 | 167 | 173 | 179 | 181 | 191 | 193 | 197 |
| 199 | 211 | 223 | 227 | 229 | 233 | 239 | 241 | 251 | 257 | 263 | 269 | 271 | 277 | 281 |
| 283 | 293 | 307 | 311 | 313 | 317 | 331 | 337 | 347 | 349 | 353 | 359 | 367 | 373 | 379 |
| 383 | 389 | 397 | 401 | 409 | 419 | 421 | 431 | 433 | 439 | 443 | 449 | 457 | 461 | 463 |
| 467 | 479 | 487 | 491 | 499 | 503 | 509 | 521 | 523 | 541 | 547 | 557 | 563 | 569 | 571 |
| 577 | 587 | 593 | 599 | 601 | 607 | 613 | 617 | 619 | 631 | 641 | 643 | 647 | 653 | 659 |
| 661 | 673 | 677 | 683 | 691 | 701 | 709 | 719 | 727 | 733 | 739 | 743 | 751 | 757 | 761 |
| 769 | 773 | 787 | 797 | 809 | 811 | 821 | 823 | 827 | 829 | 839 | 853 | 857 | 859 | 863 |
| 877 | 881 | 883 | 887 | 907 | 911 | 919 | 929 | 937 | 941 | 947 | 953 | 967 | 971 | 977 |
| 983 | 991 | 997 |
Последняя задача, которую стоит разобрать, — это алгоритм получения пифагоровых троек — трех натуральных чисел, подтверждающих теорему Пифагора, например 3, 4, 5; 5, 12, 13 и так далее, то есть таких чисел a, b и с, при которых а 2+ b 2= с 2.
Возможно, в Древнем Вавилоне знали метод нахождения пифагоровых троек, о чем свидетельствует вавилонская глиняная табличка, которую называют Plimpton 322. В ней содержится несколько троек, выраженных в шестидесятых долях. Пифагору приписывается авторство метода, позволяющего получить эти числа, основанного на гномоне квадратных чисел. Квадратное число — это то, которое можно выразить в виде квадрата (см. рисунок). Следовательно, мы имеем n ²+ (2n + 1) = (n+1) ². Для того чтобы составить пифагорову тройку, в которой катет и гипотенуза — два последовательных числа, гномон тоже должен быть квадратом, то есть 2n + 1 = k ², где k — нечетное число. Следовательно,
n = (k² - 1)/2, k нечетное.
Так можно получить тройки n = (k² - 1)/2, k, n +1 = (k² + 1)/2,
где k — нечетное число, образующее следующие таблицы.
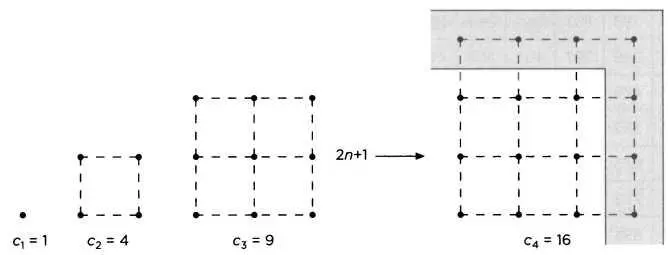
Последовательность квадратных чисел 1, 4, 9,16 (n - 1) ², n ². Чтобы перейти от c n= n ²к c n + 1= (n + 1) ², нужно добавить гномон, равный 2n +1. То есть между ними всегда будет нечетное число.
| a = k, где k нечетное | 3 | 5 | 7 | 9 | 11 | 13 | 15 | ... |
| b = n = n = (k² - 1)/2 | 4 | 12 | 24 | 40 | 60 | 84 | 112 | ... |
| c = n + 1 = n = (k² + 1)/2 | 5 | 13 | 25 | 41 | 61 | 85 | 113 | ... |
Таким образом можно получить бесконечное множество троек, но не все: например, здесь не хватает тройки 8, 15, 17, в которой разница между катетом и гипотенузой равна двум единицам.
Платону приписывают обобщение этого метода Пифагора. Необходимо перейти от (n - 1) ²к (n + 1) ². Для этого надо сложить два гномона: 2n - 1, позволяющий перейти от (n - 1) ²к n ², и 2n + 1, позволяющий перейти от n ²к (n + 1) ². Всего надо добавить 4n. То есть (n - 1) ²+ 4n = (n + 1) ². Значит, n должно быть квадратным числом: n = k ². Так мы получаем тройки k ² - 1, 2k и k ²+ 1. При k = 4 мы получим уже упомянутую тройку 8,15,17. Запишем это в виде таблицы.
| k | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |
| a = k²- 1 | 3 | 8 | 15 | 24 | 35 | 48 | 63 | |
| b = 2k | 4 | 6 | 8 | 10 | 12 | 14 | 16 | |
| с = k² +1 | 5 | 10 | 17 | 26 | 37 | 50 | 65 |
Приведенные таблицы различаются: в первой представлены простые тройки, то есть такие, у которых нет общего делителя; во второй цифры в столбцах с нечетным к можно разделить на 2, и мы получим некоторые значения первой таблицы. Можно сказать, что первая таблица включена во вторую. Но существует ли алгоритм, позволяющий получить все возможные пифагоровы тройки? Ответ на этот вопрос положительный, и дает его сам Евклид в лемме 1 книги X:
Существуют два квадратных числа, которые вместе образуют еще один квадрат.
Не вдаваясь в подробности, скажем, что Евклид использовал алгоритм α = λ ²-μ ², b = 2λμ, c = λ ²+ μ ², где λ и μ — взаимно простые числа, имеющие разную четность. Это условие необходимо соблюдать для того, чтобы тройки не повторялись и все составляющие их числа были простыми, без общих делителей. Действительно, нас интересуют только простые тройки, так как очевидно, что при любом натуральном числе k 3k, 4k, 5k тоже будут натуральными, ведь 3, 4 и 5 — натуральные. Все вышесказанное справедливо для любой пифагоровой тройки a, b, c.
ГЛАВА 8
Распространение «Начал»
Самым убедительным доказательством исторического значения труда Евклида являются многочисленные его копии и переиздания. Ни одно другое научное произведение античности не может похвастаться таким количеством переводов, изданий и комментариев.
Читать дальшеИнтервал:
Закладка:










