Josep Carrera - Трехмерный мир. Евклид. Геометрия
- Название:Трехмерный мир. Евклид. Геометрия
- Автор:
- Жанр:
- Издательство:ООО “Де Агостини”
- Год:2015
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Josep Carrera - Трехмерный мир. Евклид. Геометрия краткое содержание
Евклид Александрийский — автор одного из самых популярных нехудожественных произведений в истории. Его главное сочинение — «Начала» — было переиздано тысячи раз, на протяжении веков по нему постигали азы математики и геометрии целые поколения ученых. Этот труд состоит из 13 книг и содержит самые важные геометрические и арифметические теории Древней Греции. Не меньшее значение, чем содержание, имеет и вид, в котором Евклид представил научное знание: из аксиом и определений он вывел 465 теорем, построив безупречную логическую структуру, остававшуюся нерушимой вплоть до начала XIX века, когда была создана неевклидова геометрия.
Трехмерный мир. Евклид. Геометрия - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Прокл ничего не говорит о месте рождения Евклида, из-за чего мы можем предположить, что он о нем не знал, но рассказывает знаменитый случай о «царском пути» в изучении геометрии. Вероятно, лучшее резюме биографии Евклида сделал английский писатель Эдвард Фостер в своем путеводителе по Александрии:
«Мы ничего о нем не знаем; честно говоря, сегодня он для нас — скорее свод знаний, чем человек».
Известно, что кроме «Начал» Евклид написал и другие труды. В прологе ко второй части своего комментария Прокл приписывает ему следующие тексты:
«У него есть также много других математических сочинений, полных удивительной точности и научности. Таковы «Оптика», «Катоптрика», таковы также «Начала музыки» и книга «О делении фигур». А в «Началах» геометрии им в особенности следует восхищаться порядком и отбором приведенных теорем и задач. Ведь он берет не все, что можно сказать, а лишь самое основополагающее; кроме того, он применяет разнообразные виды силлогизмов, которые отчасти получают достоверность от причин, отчасти исходят из достоверных положений, но при этом все — неопровержимые, точные и свойственные науке. Помимо них он применяет все диалектические методы: метод разделения — при установлении видов, метод определения — при определении сущности, метод демонстрации — при переходе от начал к искомому, метод анализа — при восхождении от искомого к началам».
Люди умирают, но их труды остаются.
Последние слова математика Огюстена Луи Коши, сказанные архиепископу Парижа
Добавив к этому списку произведения, о которых упоминает Папп Александрийский (290-350) в своем «Математическом собрании», мы получим свод сочинений, приведенный в таблице на следующей странице.
В совокупности эти книги представляют собой довольно четкую программу изучения математики, а также касаются широкого ряда других вопросов геометрии (первые три — начального уровня, последние три — более сложные), астрономии, музыки, оптики и механики. Ниже приводится краткое содержание каждого сочинения, причем особое внимание мы уделим текстам по геометрии. Нам неизвестна их хронология, так что мы приводим труды в алфавитном порядке.
В «Данных» содержатся 94 предложения, в которых анализируется, какие свойства фигур можно вывести, если «известны некоторые из них». Евклид пишет, что данные могут быть нескольких типов: данные величины (касающиеся размеров), данные вида (касающиеся типа геометрических фигур) и данные положения (касающиеся их относительного расположения) или комбинация этих трех параметров. Сочинение можно назвать начальным учебником по элементарной планиметрии.
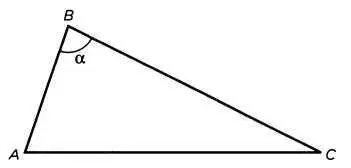
Следующий пример иллюстрирует, какие вопросы разбираются в «Данных». Здесь изданных величины мы получаем данные вида. В предложении 45 говорится:
«Если дан угол АВС [на рисунке он соответствует углу < АВС] некоего треугольника и соотношение между суммой сторон АВ и ВС данного угла и третьей стороной АС, то треугольник определен (задан)».
| Сочинения, приписываемые Евклиду | ||
| МАТЕМАТИКА | «Начала» (геометрия): книги 1—XIII (написаны Евклидом) и два апокрифа (книга XIV написана Гипсиклом, книга XV — предположительно Исидором Милетским) | |
| ГЕОМЕТРИЯ | Начальная геометрия | «Данные» |
| «О делении фигур» | ||
| «Псевдария» | ||
| Высшая геометрия | «Поверхностные места» | |
| «Поризмы» | ||
| «Конические сечения» | ||
| АСТРОНОМИЯ | «Явления» | |
| МУЗЫКА | Введение в музыку | «Гармоническое введение» (Клеонид) |
| «Деление канона» | ||
| ФИЗИКА | МЕХАНИКА | «О легкости и тяжести» |
| «О рычаге» | ||
| ОПТИКА | «Оптика» | |
| «Катоптрика» (Теон Александрийский) |
В предложениях 84 и 85 этого трактата решаются уравнения второго порядка ах ± х ²= b ²так же, как это делали месопотамские математики (мы увидим это в главе 4), когда решали следующую систему уравнений:
у±х = а,
ху = b ².
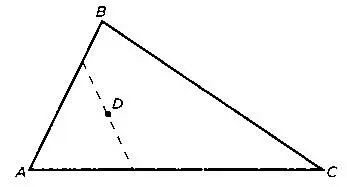
В сочинении «О делении фигур» рассматривается деление заданной фигуры одной или несколькими прямыми, «соблюдая некоторые условия», чтобы площади получившихся частей соотносились друг с другом определенным образом. Например, требуется произвести следующее деление:
Задача 20. Отделить треть треугольника ААВС с помощью прямой, которая проходит через точку D внутри треугольника.
Такие геометрические задачи скорее вписываются в математическую традицию Вавилона, чем в изложенную в «Началах». Фрагменты этого сочинения, известные нам, взяты из латинского перевода 1563 года и арабского перевода, обнаруженного в Париже в 1851 году. Единственные четыре предложения с доказательствами напоминают предложения из «Начал». Всего в сочинении содержится 36 предложений.
Сочинение «Псевдария» также не дошло до наших дней. О нем рассказывает Прокл:
«Это сочинение, в котором он дает нам такую подготовку, он назвал «Ложные умозаключения» и в нем перечислил в должном порядке их виды, дал нашей мысли упражнения в каждом виде, противопоставил лжи истину и дал опровержение лжи соответственно со способом ее проведения. Таким образом, эта книга — очистительная, имеющая целью упражнение, а «Начала» содержат неопровержимое и совершенное изложение самого научного рассмотрения предмета геометрии».
Конические сечения (или просто коники) являются пересечением конуса (двойного) с плоскостью. Тип сечения зависит от угла плоскости. Как видно на рисунке 1, если плоскость параллельна оси конуса, мы получаем гиперболу ( состоящую из двух ветвей), если плоскость параллельна образующей конуса, то параболу, а в других случаях — эллипс (включая окружность как частный случай). На рисунке 2 изображены различные конические сечения в зависимости от соотношения фокуса и директрисы.
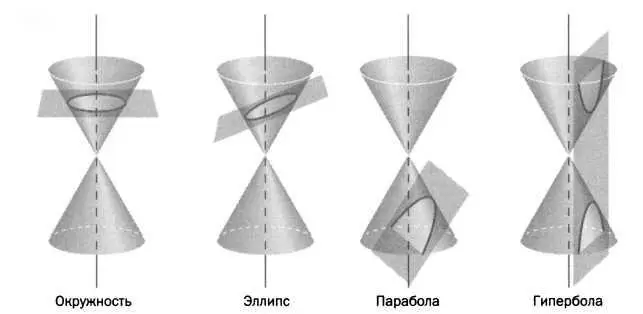
РИС. 1
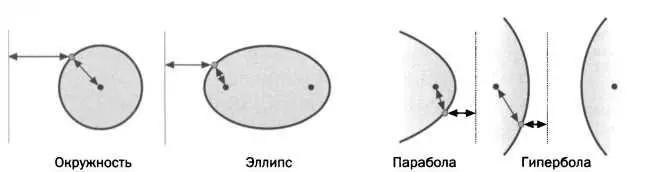
РИС. 2
Это был самый настоящий учебник, об утере которого можно только сожалеть, так как он прояснил бы, какие ошибки Евклид считал геометрическими, а какие — логическими.
Еще одно утерянное сочинение, которое цитирует Папп, — «Поверхностные места». Содержание этого свода текстов по высшей геометрии было гораздо сложнее, чем в «Началах». Как говорит Папп, в нем рассматривались «места, а точнее положение, линии или фигуры, точки которых обладают некоторым свойством» и «построение таких мест», то есть линий, например квадратрисы, цилиндрической спирали и подобных, или таких фигур, как конусы, цилиндры, сферы или полученные путем вращения конических сечений (эллипса, гиперболы и параболы). В сочинении дается такая классификация конических сечений по соотношению фокуса и директрисы, при которой не нужно прибегать к трехмерному пространству:
Читать дальшеИнтервал:
Закладка:










