Josep Carrera - Трехмерный мир. Евклид. Геометрия
- Название:Трехмерный мир. Евклид. Геометрия
- Автор:
- Жанр:
- Издательство:ООО “Де Агостини”
- Год:2015
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Josep Carrera - Трехмерный мир. Евклид. Геометрия краткое содержание
Евклид Александрийский — автор одного из самых популярных нехудожественных произведений в истории. Его главное сочинение — «Начала» — было переиздано тысячи раз, на протяжении веков по нему постигали азы математики и геометрии целые поколения ученых. Этот труд состоит из 13 книг и содержит самые важные геометрические и арифметические теории Древней Греции. Не меньшее значение, чем содержание, имеет и вид, в котором Евклид представил научное знание: из аксиом и определений он вывел 465 теорем, построив безупречную логическую структуру, остававшуюся нерушимой вплоть до начала XIX века, когда была создана неевклидова геометрия.
Трехмерный мир. Евклид. Геометрия - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
| Математики, которые, по мнению Прокла, являются предшественниками Евклида | ||
| Имя | Цитата из Прокла | Сведения из разных книг «Начал», которые предположительно были им известны |
| Фалес Милетский | Первым перенес в Элладу эту теорию. Многое открыл сам, а для многого указал путь последователям, представив одно более общим способом, другое — более наглядным. | Определение 17 из книги 1, предложения 5,15, 26 и, возможно, 32. Предложение 12 из книги III. |
| Пифагор | Преобразовал доктрину в разряд общеобразовательных дисциплин. Рассмотрел принципы геометрии с самого начала. Исследовал теоремы умозрительно, открыл иррациональные величины и строение космических тел. | Книга 1: определения 1, 3 и 6; общее понятие 5; предложения 2,17, 32, 36, 37, 45 и 47. |
| Книга II: предложения 14 и 20. | ||
| Книга III: предложения 11 и 14. | ||
| Книга IV: предложения 11,12 и 15. | ||
| Книга VI: предложения 25, 28, 29 и 31. | ||
| Книга VII: определения 3, 4, 5,11 и 13. |
| Энопид | Касался многих геометрических вопросов и многим дал наилучшее решение с использованием линейки и циркуля. | Книга 1: постулаты 1, 2 и 3, предложения 12 и 23. |
| Гиппократ | Открыл квадрируемые луночки. Написал свои «Начала». Использовал метод сведения в задаче об удвоении куба. | Книга 1: предложения 9,10,11, 12,18,19, 20, 23, 24, 25, 28, 29, 31, 32, 45 и 47. |
| Книга II: предложения 6,12,13 и 14. | ||
| Книга III: определение 11; предложения 3, 20, 21, 22, 26, 27, 28, 29, 30 и 31. | ||
| Книга IV: предложения 5, 9,15. | ||
| Книга VI: предложения 19 и 20. | ||
| Книга VII: предложение 2. Книга | ||
| XIII: предложение 12. | ||
| Феодор | Знаменитый геометр. | Результаты книги II или 1, предложение 47. |
| Платон | Математические науки получили его стараниями величайшее развитие. Его математические рассуждения пробуждают восторг в философах всех времен. | |
| Ледамант, Архит и Теэтет | Жили в одно время с Платоном. Благодаря им появились новые теоремы и геометрия стала более научной. | Результаты книг X и XIII. |
| Леонт | Составил свои «Начала» и нашел условия, при каких некоторые задачи могут быть разрешены и при каких нет. | |
| Евдокс | Увеличил число так называемых общих теорем и, воспользовавшись результатами Платона о сечениях, разработал множество их видов. | Книга V:определения 4 и 5 и общие предложения. |
| Книга X: предложения 1 и 2. | ||
| Книга XII: предложения 5,6, 7 и 10. | ||
| Менехм и Динострат | Первый был учеником Евдокса, второй известен как его брат. Сделали геометрию еще более совершенной. | |
| Филипп из Менде | Работал под руководством Платона. С ним геометрия достигла зрелости. |
Сочинение Прокла написано под явным влиянием «Истории геометрии» Евдема Родосского и неоплатонизма. В нем не указаны имена астрономов — последователей Евдокса, не упоминаются перипатетики и сам Аристотель, а также Аристей Старший, который, возможно, был отцом учения о конических сечениях и геометрических местах. В нем нет Гиппаса из Метапонта и Филолая, нет софистов Антифонта, Брисона и Гиппия Элидского, нет атомистов Парменида, Зенона и Демокрита и даже Автолика Питанского, наконец, в комментариях не сказано ни слова об ученых-арифметиках. И все же этот текст заслуживает пристального внимания.
Фалесу и Пифагору различные авторы приписывают одни и те же достижения, а в случае с Гиппократом мы опираемся на свидетельство римлянина Симпликия, в свою очередь ссылающегося на «Историю геометрии» Евдема.
ГЛАВА 2
Структура «Начал»
Не меньшее значение, чем содержание, имеет структура «Начал»: Евклид отталкивается от краткого списка гипотез и переходит к дедуктивному доказательству многочисленных предложений. Такой подход сообщает этому произведению основательность, кажущуюся непогрешимой. Однако этот крепкий фундамент евклидового здания состоит в том числе и из кирпичиков общих представлений о математике, восходящих к философии Платона и Аристотеля.
«Начала» являются прямым наследием философии Платона и Аристотеля. По Платону, материальные объекты также являются идеальными, то есть существуют в мире идей. Аристотель возражал против этого, и можно утверждать, что текст Евклида написан под влиянием Аристотеля. И все же платоновская философия математики особо изучалась в Академии, о чем свидетельствует надпись над входом: «Да не войдет сюда не знающий геометрии».
Мы же ограничимся комментарием к аналогии разделенной линии, о которой Платон пишет в шестой книге «Государства» (см. схему на следующей странице). Существуют три воплощения предмета «кровать»: «кровать, созданная Богом», «кровать, сделанная плотником» и «кровать, нарисованная художником». «Бог, — говорит Платон, — желая быть истинным создателем истинно существующей кровати, [...] создал ее по природе своей единственной». Плотник же делает копии. А художник копирует плотника, но не «настоящую кровать».
В этом примере затрагивается вопрос существования, один из основных в платоновской философии, поскольку, по Платону, невозможно от эпистемологии (то есть знания или познания) перейти к онтологии (реальности, являющейся предметом познания). Он задается следующими вопросами: все ли кровати реальны, или же только некоторые, или ни одна? Что мы подразумеваем под «реальным», точнее, о какой реальности мы говорим, когда утверждаем, что научное знание состоит в «истинном познании реальности»? Если мы сузим вопрос до области математики, то как надо понимать математические объекты (вопрос эпистемологического характера) и что мы можем сказать об их существовании (проблема онтологического характера)?
По Платону, есть две реальности: реальность умопостигаемого мира идей, которую можно познать истинным знанием, и зримая реальность окружающего нас мира, о которой можно иметь лишь мнение. Приводя аналогию с разделенной линией, философ говорит об умопостигаемом, имея в виду, что мы можем понять только верхний уровень линии, неизменный уровень идей, нижний же отрезок относится к изменчивому миру, и о нем мы можем только составить мнение.
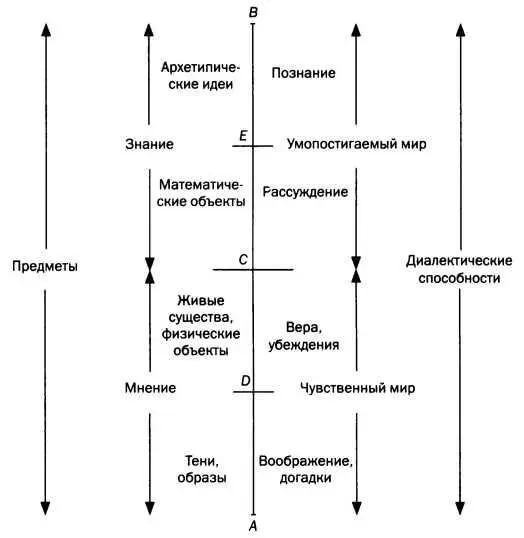
Разделенная линия, книга VI «Государства» Платона.
Афинская Академия была основана Платоном около 388 года до н.э. как философская школа. Она была построена в садах Академа, легендарного героя греческой античности, в последний раз возрождалась после смерти Прокпа в 485 году и была окончательно закрыта в 529-м по приказу императора Юстиниана. В стенах Академии разворачивалась основная философская и научная деятельность той эпохи. Там изучали медицину, совершенствовались в риторике и углублялись в астрономию, уделяя особое внимание гелиоцентрической теории. По всем этим дисциплинам разворачивались открытые дискуссии.
Читать дальшеИнтервал:
Закладка:










