Мэтью Джексон - Человеческие сети [Как социальное положение влияет на наши возможности, взгляды и поведение]

Такое рода обдумывание более чем естественно, иногда именно оно и является идеальным способом обработки информации — достаточно вспомнить о том, как Гальтон обнаружил, что среднее значение от всех предложенных догадок весьма близко к правде. Однако в вашем случае процесс на этом не заканчивается. Ваши друзья беседуют не только с вами, так что со временем и они могут поменять мнение. А в их новых мнениях отразится новая информация, полученная ими от других участников вашей сети, включая людей, которые не являются вашими друзьями. Поэтому имеет смысл через некоторое время снова поговорить с друзьями на ту же тему. Тогда после повторного разговора вы опосредованно получите и информацию от друзей ваших друзей.

Если речь идет о весе быка, скорее всего, эта тема быстро всем наскучит и после пары итераций (в лучшем случае) процесс обсуждения затухнет. Зато на другие, более животрепещущие, темы — например, о том, какова вероятность, что вакцина навредит вашему ребенку, или о том, насколько интенсивно нужно заниматься спортом, чтобы сохранять здоровье, — с людьми можно говорить практически бесконечно. Со временем ваши представления вберут в себя информацию, полученную в дружеских беседах через третьи (и так далее) руки.

Процесс этот показан на рисунке 7.1.

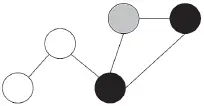
(a) Первоначальные оценки — еще до разговоров. Более светлые тона — более легковесные оценки. Средний оттенок серого означает верную догадку.

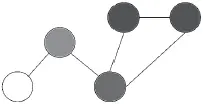
(b) После того как люди поговорили с каждым из друзей, они переосмысляют свои оценки. Их новые оценки являются чем-то средним между их прежними оценками и первоначальными оценками их друзей. Многие из них теперь приобрели тот или иной оттенок серого. Человек (кружок) в нижнем левом углу еще совсем не переменил мнение — потому что и он сам, и его друг начали с одинаковой заниженной оценки. А человек, начавший с верной оценки, даже потемнел, склонившись в сторону переоценки, потому что он дружит с двумя людьми, начавшими с переоценки.

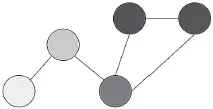
(c) Люди побеседовали еще раз и снова скорректировали оценки. Большинство теперь тяготеет к среднему оттенку серого, но человек в нижнем левом углу все еще сохраняет очень светлый оттенок серого.

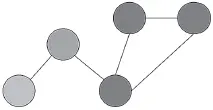
(d) Представления все больше сближаются.

Рис. 7.1. Обмен мнениями в сети. Пять человек в сети прикидывают, сколько весит бык, весящий в действительности 1200 фунтов. Два человека (в левой части схемы), с белыми узлами, начинают с недооценки веса быка — выдвигают предположение, что он весит 1000 фунтов. Два человека с черными узлами начинают с переоценки — они полагают, что бык весит 1400 фунтов. Человек с серым узлом начинает с очень удачной догадки — 1200 фунтов. Итак, чем светлее тон, каким закрашен кружок-узел, тем ниже предположительный вес быка. Люди несколько раз беседуют с друзьями — и каждый раз выводят новое среднее значение, исходя из своих прежних оценок и последних догадок друзей.

Процесс, представленный на рисунке 7.1, показывает, что обмен мнениями в сети имеет сходство с диффузией и заражением. Если каждый из нас разговаривает с несколькими друзьями, в итоге этот разговор быстро «расширяется», охватывая все больше людей, и после всего нескольких итераций к нам уже косвенным образом поступает информация от всех, кто входит в более широкую сеть. Благодаря сетевому эффекту «тесного мира» достаточно всего нескольких итераций, чтобы информация, исходящая от одного человека, достигла большинства других — пускай даже в несколько «разбавленном» виде.

Такого рода познание, при котором каждый человек многократно беседует с друзьями и просто продолжает выводить некое среднеарифметическое, отталкиваясь от их мнений, получило название «дегроотовского познания» — в честь статистика Морриса Дегроота {257}. Дегроотовская модель не предполагает, что люди произвольно проделывают сложные вычисления, — нет, речь о простых действиях, вроде выведения среднего арифметического значения. Пожалуй, не удивительно, что когда нужно предсказать действия реальных людей, даже в простых сетях, дегроотовская модель обнаруживает больше сходства с поведением людей, чем какая-нибудь всеведущая и замысловатая модель, согласно которой люди, обрабатывая информацию, делают поправки на время и реагируют на изменение чужих мнений, — во всяком случае, в некоторых типах среды, о чем мы еще поговорим.

Однако даже дегроотовское познание сложнее, чем простая диффузия, так как оно требует напряжения и многократных бесед.

Способность человека влиять на представления других людей и менять их зависит от его центральности в сети. Здесь действует парадокс дружбы (о котором шла речь в главе 2). Люди, у которых больше друзей, в итоге сверяют свои мнения с мнениями большего количества людей. В сети, показанной на рисунке 7.1, человек, обозначенный черным кружком внизу картинки, занимает наиболее центральное положение по любым критериям центральности. Хотя среднее значение от всех первоначальных оценок в этом примере составило бы в точности 1200 фунтов, уже в силу того, что люди, обозначенные темными кружками, то есть предложившие в качестве догадки более высокие значения, обладают большей центральностью, чем люди, обозначенные белыми кружками и склонившиеся в пользу меньшего веса быка, — консенсусная величина в итоге слишком подскочила вверх, и предполагаемый вес оказался завышен.

Итак, чем больше мнений «центральных» людей, тем больше они влияют на мнения остальных. Если вы вспомните наш разговор о центральностях, то подумаете, что, поскольку люди беседуют снова, снова и снова… то по-настоящему важна не столько чья-то центральность, сколько просто чья-то центральность по собственному вектору. И будете правы. Если я дружу с другими людьми, у которых множество связей, значит, до них дойдет мое мнение, а затем от них распространится дальше, вширь, — и, следовательно, иметь друзей, имеющих множество связей, не менее важно, чем просто иметь много друзей. Иначе говоря, степень участия первоначального мнения каждого человека в итоговом общем мнении, которое закрепляется в обществе, если это общество продолжает многократно выводить «среднее арифметическое», в точности пропорционально центральности по собственному вектору этого человека {258}.