Александр Невеев - Ловушки разума и Ловцы душ. Убеждения, меняющие нашу жизнь, или Что заставляет нас купить дырку от бублика

При этом в рамках эффекта Джин Диксон подчеркивается, что люди запомнят именно сбывшиеся предсказания, а количество несбывшихся их интересовать не будет.

Понятно, что такой подход, жертвой которого, кстати, может пасть любой человек, совершенно иррационален. Если предсказатель сделал 1000 предсказаний и из них сбылось всего 100, то эффективность такого предсказателя составляет 10 %. Имеет ли смысл платить за предсказания, которые сбываются лишь в 10 % случаев? А ведь это подразумевает, что в 90 % случаев предсказание не сбывается, то есть девять из десяти раз вы потратите деньги зря или даже во вред себе, поскольку неверное предсказание помешает вам действовать правильно.

Более того, факт, что предсказания сбылись в столь малом числе случаев, может говорить и о том, что сбылись они чисто случайно, то есть слова предсказателя случайно совпали с тем, что произошло в действительности. И как вы понимаете, на самом деле именно так и обстоят дела.

Несмотря на то что в названии эффекта Джин Диксон используется имя известной предсказательницы, этот эффект наблюдается не только в случае предсказаний.

По сути, шарлатаны, продающие чудодейственные снадобья и различные рецепты успеха, тоже живут за счет этого эффекта. Если такое снадобье помогло хотя бы нескольким людям, то именно об этом будут кричать шарлатаны, их рекламные ролики и тексты, их сайты и пр. Да и убеждать людей покупать шарлатанские снадобья и услуги будут именно эти случаи.

Какие выводы сделал бы потенциальный шарлатан, прочитав об эффекте Джин Диксон?

Очень простые:

• чем больше я делаю предсказаний, тем выше вероятность того, что они сбудутся;

• чем большему количеству людей я предлагаю мое снадобье и чем от большего количества болезней это снадобье, по моим словам, помогает, тем выше вероятность того, что появятся люди, которые заявят: «А мне помогло!»;

• чем большему количеству людей я предлагаю решать проблемы с помощью моих «экстрасенсорных способностей» и чем больше вариантов проблем предлагаю решать, тем выше вероятность появления людей, уверенных, что я экстрасенс и что именно я помог им решить их проблемы.

Наверное, не существует человека, который не слышал бы о золотом сечении. Чуть меньшее число людей не просто слышали о нем, но и знают и могут объяснить, что это такое.

Золотое сечение – это что-то вроде универсального правила достижения красоты в живописи, архитектуре и, говорят, даже в музыке. Точнее, это даже не правило, а, скорее, универсальная пропорция, соотношение частей между собой и с целым, которое совершенно точно будет выглядеть красиво. Каково же это соотношение?

Золотое сечение будет иметь место тогда, когда целое относится к большей части так же, как большая часть относится к меньшей части.

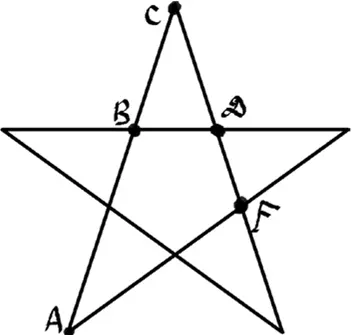
Примером фигуры, построенной по принципу золотого сечения, является обычная пятиконечная звезда.

Действительно, в пятиконечной звезде AC относится к АВ так же, как CF относится к DF.

Что-то похожее на золотое сечение существует и в мире случайностей и вероятностей. И называется это «золотое сечение мира случайностей» нормальным распределением .

Но прежде чем говорить о нормальном распределении, о законе нормального распределения, знание которого может защитить нас от попадания в целый ряд ловушек разума, нужно продвинуться еще на один шаг в исследовании мира случайностей.

Однажды (в первой четверти XVII века) Козимо II Медичи – великий герцог Тосканский – обратился к Галилео Галилею с вопросом о том, почему в некой игре с тремя игральными костями десять очков выпадает чаще девяти.

Будучи умнейшим человеком, Галилей не только нашел ответ на этот вопрос, но и написал целый научный труд под названием «Рассуждения об игре в кости», который стал значимой вехой на пути познания человеком мира случайностей и вероятностей. Да-да, Галилей не только кидал предметы с Пизанской башни, не только с помощью изобретенного им телескопа рассмотрел и описал поверхность Луны и открыл спутники Юпитера, но и внес вклад в развитие теории вероятностей.

Почему же десять очков выпадает при бросании трех игральных костей чаще, чем девять?

Вы хорошо поняли, что если вас спросят о том, что более вероятно при однократном подбрасывании монеты – выпадение орла или выпадение решки, то правильным ответом будет «вероятности равны». Тот же ответ будет правильным и в случае, если мы бросаем одну игральную кость: вероятность выпадения каждого очка (от единицы до шестерки) одинакова и составляет 1/6, или примерно 16 %.

А что, если мы поговорим о бросании двух игральных костей, как это происходит, например, в нардах? Что более вероятно: выпадение двойки или выпадение тройки?

Давайте рассуждать. Когда мы получим двойку? Это очень просто: двойка выпадает, когда на одной кости выпадает единица и на другой кости тоже выпадает единица.

А когда выпадает тройка? Это тоже просто: когда на одной кости выпадает единица, а на другой – двойка.

Отсюда следует, что вероятности выпадения двойки и тройки при бросании игральных костей равны.

Правильно?

Нет, неправильно!

Дело в том, что двойку действительно можно выбросить только одним способом: на одной кости выпадает единица и на другой единица. А вот тройку можно выбросить двумя способами, то есть способов получения тройки больше, а значит, эта комбинация более вероятна.

Почему тройка получается двумя способами? Потому что одним таким способом будет комбинация «один-два», а другим – комбинация «два-один». Это легче представить, если мы раскрасим кости в разный цвет.

Вот единственный способ получения двойки.

А вот два способа получения тройки.

Обратите внимание!Если бы вас спросили, какая комбинация, возникающая при бросании двух игральных костей, более вероятна:

правильным ответом был бы «комбинации выпадают с равной вероятностью». Действительно, если говорить о комбинациях, а не об их числовых значениях (очках, получаемых при выпадении комбинации), то при бросании двух игральных костей существует всего 36 равновероятных комбинаций (две кости, у каждой из которых шесть граней, то есть 6 2= 36).