Джо Боулер - Безграничный разум

Слабые ученики решали ее с помощью обратного счета, то есть выбирали более трудный путь (попробуйте-ка начать с 16 и отсчитать 13 чисел в обратном порядке); при этом вероятность ошибки довольно высока. Сильные ученики действовали гибко, вычитая 3 из 6 и 10 из 10, получали ответ 3. Подобная гибкость в обращении с числами предельно важна, но если учеников обучают слепо заучивать математические факты и применять математические методы без понимания их сути, то они автоматически обращаются к тому, что вызубрили, и никогда не разовьют способность концептуально размышлять о числах и гибко взаимодействовать с ними.

Часто с отстающими учениками начальной школы занимаются дополнительно и отдельно от других, особенно если у них проблемы со счетом, — подход под названием «тренировать и готовить» сами ученики метко переименовали в «тренировать и убивать». Это последнее, что им нужно. Такие ученики не успевают по математике из-за неправильного подхода к обучению, думая, что им необходимо опираться на запоминание. Даже в тех случаях, когда чувство числа принесло бы им больше пользы, они продолжают применять методы счета, основанные на заучивании. Вместо того чтобы заниматься зубрежкой, им необходимо научиться гибко и творчески обращаться с числами. Они должны подходить к числам по-другому — концептуально.

Что это значит — подходить к числам концептуально? Многим читателям, кому внушали, что нужно запоминать математические методы и факты, это может показаться чужеродной идеей. Грей и Толл разграничили концепции и методы (рис. 5.3).

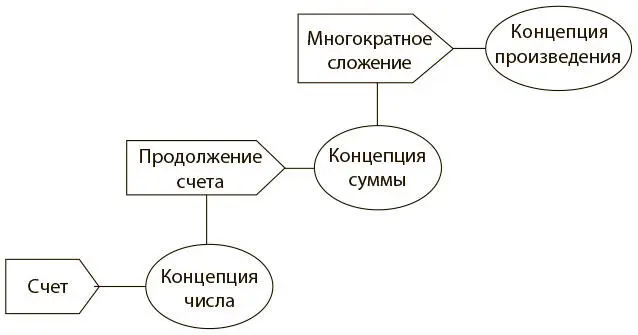
Рис. 5.3. Математические методы и концепции

Мы изучаем такие методы, как счет, чтобы сформировать концепцию числа — представление о нем. Мы осваиваем метод продолжения счета, чтобы воспринять концепцию суммы, а усвоив метод многократного сложения, мы поймем концепцию произведения.

Математика — концептуальный предмет, но многие ученики не видят ее в таком ракурсе. Математика для них — это набор правил или методов, которые нужно запомнить. Как мы уже обсуждали, такой подход становится в итоге серьезной проблемой, и некоторые исследования мозга проливают свет на причины, по которым это происходит.

Когда вы изучаете область, о которой ничего не знаете, она занимает много места в вашем мозге: ведь вам нужно напряженно размышлять, как это работает и как разные концепции соотносятся друг с другом. Но математические понятия, которые вы изучили ранее и хорошо знаете (например, сложение), занимают в мозге небольшое пространство. Вы можете использовать эти знания, даже не задумываясь. Процесс сжатия происходит потому, что головной мозг — крайне сложный орган, контролирующий много разных процессов, и в один момент он может сосредоточиться только на нескольких несжатых концепциях. Те же, которые вы хорошо знаете, сжимаются и архивируются. Уильям Тёрстон, выдающийся математик, получивший Филдсовскую премию, так описывает процесс сжатия.

Математика поразительно легко поддается сжатию: вы можете долго и напряженно трудиться, шаг за шагом прорабатывая один процесс или идею с нескольких точек зрения. Но как только вы по-настоящему поймете нечто и сможете увидеть это как единое целое, скорее всего, произойдет очень сильное ментальное сжатие. Вы можете отправить эту информацию в архив, а при необходимости быстро и полностью восстановить и использовать ее всего лишь за один шаг в рамках другого ментального процесса. Озарение, которым сопровождается такое сжатие, — одна из истинных радостей [129].

Многие ученики не считают, что математика дарит подлинную радость, — отчасти потому, что в их мозге сжатия не происходит. Мозг способен сжимать только концепции, но не правила и методы. Следовательно, у учеников, которые не мыслят концептуально, а воспринимают математику как список правил, подлежащих запоминанию, сжатия не происходит и их мозг не может упорядочивать концепции и архивировать их, а пытается хранить длинные списки методов и правил [130]. Вместо сжатых концепций их знания больше напоминают лестницу, состоящую из нагромождения заученных методов и, как им кажется, ведущую наверх. Именно поэтому важно воспитать концептуальный подход к математике — основу математического мышления.

Когда я рассказываю учителям и родителям об этом исследовании, они задают вопрос: «Как сделать так, чтобы мои ученики воспринимали информацию концептуально?» Существует много способов научить детей размышлять на концептуальном уровне. Во-первых, важно донести до них причины, почему работают те или иные методы, а не просто предлагать заучивать их. В предыдущей главе мы говорили о том, насколько важно задавать ученикам вопросы об их в и дении той или иной идеи и убеждать их в том, что это действительно способствует ее концептуальному пониманию.

Еще один концептуальный подход к преподаванию и изучению математики, названный «Беседы о числах», был задуман преподавателями Рут Паркер и Кэти Ричардсон и разработан Кэти Хамфриз и Шерри Пэрриш. Метод состоит в обсуждении чисел и позволяет ученикам младших и средних классов развивать чувство числа и понимать гибкую и концептуальную природу математики. В ходе обсуждений ученикам предлагают совершить вычисления в уме, не используя бумагу и ручку. Затем учителя собирают информацию о том, какие методы счета использовали ученики.

Обучая других проводить беседы о числах, я, помимо прочего, рекомендую применять визуальные решения, чтобы активировать разные нейронные связи в мозге. Чтобы понять это, попробуйте вычислить в уме, сколько будет 18 × 5, до того как вы прочитаете или подсмотрите пути решения.

На рис. 5.4 приведены шесть разных способов вычисления 18 × 5 (на самом деле их больше) с визуальными решениями.

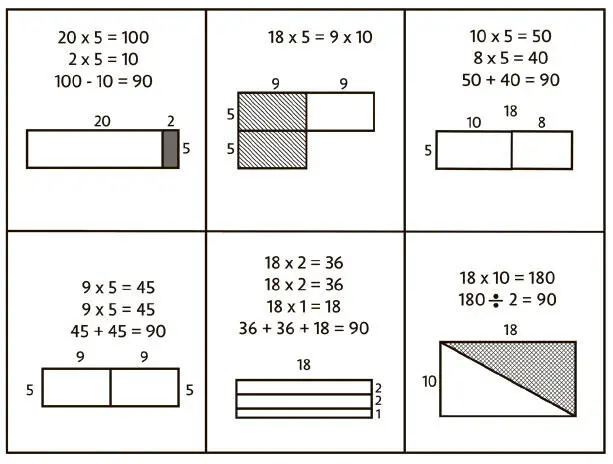
Рис. 5.4. Шесть визуальных решений задачи на умножение

Можно обозначить все проблемы с числами и решать их по-разному, разбивая числа на суммы или произведения и приводя к более «удобным» для счета числам, например 20, 10, 5 или 100. Это упрощает вычисления и способствует гибкости в обращении с числами, лежащей в основе чувства числа. Ученики любят рассказывать о своих стратегиях; как правило, они увлеченно и с интересом анализируют разные методы, используемые при решении задач. Они осваивают ментальную математику, у них появляется возможность запомнить факты, а также формируется концептуальное понимание чисел и арифметических свойств, что крайне важно для успешного изучения алгебры и других разделов математики.