Наталья Бурханова - Теплотехника

Если произвести замену удельных газовых постоянных R 1, R 2, …, R n их значениями из уравнения Клайперона, найдем среднюю молярную массу смеси газов, если смесь определяется массовыми долями:

M = 1 / (r 1 / M 1 + r 2 / M 2 +. + r n / M n).

В случае, когда смесь определяется объемными долями, получаем следующее выражение:

R = 1 / еr iR i = 8314,2 / еr iM i.

Зная, что R = 8314,2 / M, получим:

M = еr iM i = r 1M 1+ r 2M 2+. + r nM n.

Таким образом, средняя молярная масса смеси газовопределяется суммой произведений объемных долей на молярные массы отдельных газов, из которых состоит смесь.

Давление, записанное в виде: P i=N ikT / V,

где i = 1,2,..., r, называется парциальным.Здесь r – число газов в смеси;

N i – число молекул i-го газа;

V – объем смеси;

k – постоянная Больцмана;

Т – температура.

Оно может быть найдено, если все основные параметры газа известны:

P i= m iR iT / V =m iR i / mR = Pg iR i / R = Pg iM / M i

Если смесь задается объемными долями, то для получения парциального давления каждого газа обращаются к закону Бойля-Мариотта, из которого можно найти, что при Т = const:

P iV = PV i и P i= PV i / V = r iP.

Парциальное давлениелюбого газа вычисляется как произведение общего давления смеси газов на его объемную долю. Последнее уравнение используют при решении технических задач и при проверке тепловых установок. Объемные доли газов получают на опыте, используя газоанализаторы.

Физический смысл парциального давления Pi состоит в том, что это есть давление i-го газа при условии, что он занимал бы объем V.

Закон Дальтонаотражает зависимость между давлением смеси идеальных газов и их парциальными давлениями. Он гласит: давление смеси r идеальных газов и сумма их парциальных давлений равны между собой. Математическая формулировка закона Дальтона выглядит следующим образом:

Р = Р 1+ Р 2+ ...+ P r = NkT / V,

где N = N 1 + N 2 +... + N r – число молекул в смеси r газов.

Давление, которое оказывают молекулы каждого из r идеальных газов, не зависит от давления, оказываемого молекулами остальных газов. Причина такого явления заключается в том, что молекулы в идеальном газе не взаимодействуют. Было показано на опыте, что на высоких давлениях (порядка Ю 6Па) закон Дальтона не выполняется.

Первый закон термодинамики основан на всеобщем законе сохранения и превращения энергии, который устанавливает, что энергия не создается и не исчезает.

Тела, участвующие в термодинамическом процессе, взаимодействуют друг с другом путем обмена энергией. При этом у однихтел энергия уменьшается, а у других – увеличивается. Существует два варианта передачи энергии физическими телами: теплообмен и совершение механической работы.

На практике единицей работы является также джоуль, количество работы обозначается L, удельная работа на единицу массы П кг) обозначается /.

Существует несколько основных положений первого закона термодинамики.

L Любые виды энергии не возникают сами по себе, а взаимно превращаются друг в друга, причем их количества всегда одинаковы.

2. Невозможно построить вечный двигатель первого рода.

3. Если система полностью изолирована, то ее внутренняя энергия остается постоянной.

Предположим, что Q – количество теплоты, подведенное к телу, которое необходимо затратить на осуществление работы и на преобразование внутренней энергии:

Q = ΔU +L,

где L = ml – количество работы;

ДU = mДu– разность внутренней энергии начального и конечного состояния;

Q = mq.

В случае массы тела, равной 1 кг:

q = Δ u+l,

где l, q, Du – удельные количества работы, теплоты, разность внутренних энергий начального и конечного состояния. Если процесс бесконечно малый, то

dq = du + dl.

Полученное соотношение является математической моделью первого закона термодинамики.Отсюда следует такая формулировка закона: «Все количество теплоты, которое получает физическое тело, тратится на выполнение работы и на преобразование внутренней энергии тела».

Существует так называемое правило знаков для параметров: q > 0, если теплота подводится к физическому телу, и q <0, если отводится; l > 0, если работа совершается самим телом (расширение), и l < 0, если работу совершают над телом извне (сжатие); D u > 0 – если внутренняя энергия тела увеличивается, D u < 0 – если внутренняя энергия уменьшается.

Внутренняя энергияскладывается из внутренних кинетической и потенциальной энергий. Внутренняя кинетическая энергия создается хаотическим движением молекул вещества.

Кинетическая энергия всей макросистемы вычисляется:

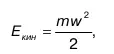
где m – масса системы;

w – скорость ее движения в пространстве.

Силы взаимодействия молекул вещества друг с другом определяют внутреннюю потенциальную энергию тела.

Внутренней энергиейназывается такая энергия, которая заключена в самой системе и имеет две составляющие – кинетическую энергию.

Изменение удельной потенциальной (внутренней) энергии того же тела. Изменение всей удельной (внутренней) энергии при термодинамическом процессе будет выглядеть так:

Δu – U k – и р.

Внутренняя энергия рабочего тела произвольной массы при этом рассчитывается по формуле:

Δv-V k– V p.

Предположим, что рабочее тело переходит из первого состояния во второе при подводе теплоты извне. Тогда количество этой теплоты выразится в виде:

q 1, 2– u 2- U 1.

Процесс проходит по изохорному закону, имеем:

q 1,2= ć v (T 2-T 1).

В общем виде для любого вещества массой m:

v 2-v 1– mć v(T 2– T 1),

где T 1– начальная температура термодинамического процесса;

T 2 – конечная температура;

u 1– начальная величина внутренней энергии;

u 2– конечная величина внутренней энергии;

ć– средняя удельная теплоемкость (изохорная).

Газ получает теплоту от определенного источника вне системы. обозначим давление газа буквой р, площадь поршня – S, тогда под действием внешней силы F = pS на поршень он будет неподвижен. При уменьшении внешней силы F разность этих двух сил pS – F сместит поршень вправо. Газ под поршнем будет расширяться и преодолевать внешние силы, совершая при этом работу. При равновесном процессе имеем следующее.