Джеймс Глик - Хаос. Создание новой науки

Фейгенбаум.

Свитанович.

Сама точка является нульмерной, одномерно все фазовое пространство системы – ее состояние в фиксированный момент времени характеризуется одним числом.

Форд.

Стипендия Макартура, а в 1986 году премия Вольфа в области физики.

Дайсон.

Гилмор.

Свитанович.

Но даже тогда доказательство было не вполне строгим в том смысле, что оно зависело от огромного количества вычислений, которые не могли быть сделаны или проверены без использования компьютера. Лэнфорд; Lanford О. Е. «A Computer-Assisted Proof of the Feigenbaum Conjectures» // Bulletin of the American Mathematical Society. Vol. R 427; а также: Collet P., J.-P. Eckmann J.-R, Lanford E. «Universal Properties of Maps on an Interval» // Communications in Mathematical Physics. Vol. P. 211.

Фейгенбаум; «The Discovery of Universality». P. 17.

Форд, Фейгенбаум, Лебовиц.

Форд.

Фейгенбаум.

Либхабер, Каданов.

Либхабер.

Libchaber A. «Experimental Study of Hydrodynamic Instabilities. Rayleigh-Benard Experiment: Helium in a Small Box» // Nonlinear Phenomena at Phase Transitions and Instabilities / Ed. by T. Riste. New York: Plenum, P. 259.

Либхабер, Фейгенбаум.

Либхабер.

Либхабер.

Stevens W. «This Solitude of Cataracts» // The Palm at the End of the Mind/ Ed. by Holly Stevens. New York: Vintage, R 321.

Stevens W. «Reality Is an Activity of the Most August Imagination» // Ibid. R 396.

Schwenk T. Sensitive Chaos. New York: Schocken, P. 19.

Перевод Я. Пробштейна.

Ibid.

Ibid. R 16.

Ibid. R 39.

Thompson D. W. On Growth and Form / Ed. by J. T. Bonner. Cambridge: Cambridge University Press, R 8.

Ibid. P. viii.

Gould S. J. Hen's Teeth and Horse's Toes. New York: Norton, P. 369.

On Growth and Form. P. 267.

Ibid. P. 114.

Кэмпбелл.

Либхабер.

Либхабер и Море, 1980 и 1981 годы. Ясное краткое изложение дается также в предисловии Свитановича.

Хоэнберг.

Фейгенбаум, Либхабер.

Голлаб.

Литература на этот счет равно обширна. См. краткое изложение ранних попыток соединить теорию и опыт в различных системах: Swinney H. L. «Observations of Order and Chaos in Nonlinear Systems» // Physica. Vol. 7D. R 3-Cyинни приводит список источников, разделенный на категории от электронных и химических осцилляторов до менее очевидных экспериментов.

Franceschini V., Tebaldi С. «Sequences of Infinite Bifurcations and Turbulence in a Five-Mode Truncation of the Navier-Stokes Equations» //Journal of Statistical Physics. Vol. R 707–726.

Collet R, Eckmann J.-R, Koch H. «Period Doubling Bifurcations for Families of Maps on R n» // Journal of Statistical Physics. Vol. R 1.

Либхабер.

Барнсли.

Барнсли.

По-английски действительные числа называются real ( numbers ), а мнимые – imaginary , что можно также перевести как «настоящие», или «реальные», и «воображаемые» соответственно.

На самом деле интегрируются функции комплексной переменной.

Хаббард; Douady A. «Julia Setsand the Mandelbrot Set». P. 161-В основном тексте «Красоты фракталов» также приводится краткий математический обзор метода Ньютона, равно как и других встречающихся теорий комплексных динамических систем, обсуждаемых в этой главе.

«Julia Sets and the Mandelbrot Set». R 170.

Хаббард.

Хаббард; The Beauty of Fractals; Richter P. H., Peitgen H.-O. «Morphology of Complex Boundaries» // Bunsen-Gesellschaft für Physikalische Chemie. Vol. R 575–588.

Например, Хаббард. Доступное введение в тему с рекомендациями, как самостоятельно написать программу для микрокомпьютера: Dewdney A. К. «Computer Recreations» // Scientific American. August P. 16-Пайтген и Рихтер в «Красоте фракталов» предложили детальный обзор как математических расчетов, так и некоторых наиболее зрелищных доступных изображений.

«Julia Sets and the Mandelbrot Set». R 161.

Мандельброт, Лафф, Хаббард. Работа Мандельброта, написанная им от первого лица: «Fractals and the Rebirth of Iteration Theory» // The Beauty of Fractals. P . 151–160.

Мандельброт; The Beauty of Fractals.

Мандельброт.

Хаббард.

Пайтген.

Хаббард.

Рихтер.

Пайтген.

Пайтген.

Йорк; хорошее введение в тему для тех, кто разбирается в технических деталях: MacDonald S. W., Grebogi С, Ott E., Yorke J. A. «Fractal Basin Boundaries» // Physica. Vol. 17D. R 125–183.

Компьютерная программа, воспроизводящая множество Мандельброта, состоит из нескольких существенных частей. Главный ее механизм заключается в цикле, в котором выбирается начальное комплексное число и к нему применяется арифметическое правило. Для множества Мандельброта правило таково: z → z 2+ с, где начальное значение z равно нулю, а с представляет собой комплексное число, соответствующее тестируемой точке. Итак, возьмем нуль, умножим его сам на себя, прибавим начальное число; взяв результат (он совпадет с начальным числом), умножим его сам на себя и прибавим начальное число; возьмем новый результат, опять умножим его сам на себя и прибавим начальное число. Арифметика комплексных чисел довольно бесхитростная. Комплексное число состоит из двух частей: например, 2 + 3i (местоположение точки: 2 к востоку и 3 к северу на комплексной плоскости). Чтобы сложить два комплексных числа, надо лишь сложить действительные части для получения новой действительной части и мнимые – для получения новой мнимой части:

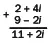
Чтобы перемножить два комплексных числа, нужно умножить каждую часть одного из них на каждую часть другого и сложить получившиеся четыре результата. Поскольку i , умноженное само на себя, в силу первоначального определения мнимых чисел дает −1, то один член результата переходит в другой:

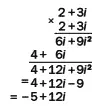
Чтобы выйти из этого цикла, программа должна отслеживать текущий итог. Если результат стремится к бесконечности, все более и более удаляясь от центра плоскости, выбранная точка не принадлежит множеству. В том случае, когда итог превышает 2 или становится меньше −2 либо в действительной, либо в мнимой части, результат, бесспорно, стремится к бесконечности и работа программы может продолжаться. Если она выполняет одни и те же вычисления много раз, не превышая 2, точка принадлежит множеству. Число итераций зависит от степени увеличения. Для масштаба, доступного персональному компьютеру, ста или двухсот повторений часто бывает достаточно, а тысяча дает полную гарантию. Программа должна повторить данный процесс для каждой из тысяч точек решетки, масштаб которой можно «подкрутить» для большего увеличения. Затем программа должна показать полученный результат. Точки, входящие в множество, могут быть обозначены черным цветом, а не принадлежащие к нему – белым. Для получения более наглядного изображения белый цвет можно заменить оттенками других цветов. В частности, если итерирование прекращается после десяти повторений, программа должна выдать красную точку, после двадцати – оранжевую, после сорока – желтую и так далее. Цвета и момент остановки расчета точек программист может выбрать сам. Цвета надлежащим образом обозначают контуры «ландшафта», оставшегося за пределами множества. – Прим. автора.