Рудольф Ташнер - Число, пришедшее с холода. Когда математика становится приключением

Ферма не смог подтвердить этот феномен при показателе степени 4, однако закономерность имела место при показателях 5, 3 или 7. Числа 3, 5 и 7, подумал Ферма, простые. 4 таким числом не является. Может быть, дело именно в этом?

Эта мысль уже не отпускает Ферма. Если обозначить простое число символом p , то, возможно, для каждого числа a разность a p — a делится без остатка на простое число p .

Изысканное рассуждение, развитое современником и другом Ферма по переписке Блезом Паскалем, утвердило Ферма в его дальнейших предположениях.

Что произойдет, спросил себя Ферма, если брать не p -ю степень числа a , то есть число a p , а вычислить p -ю степень следующего числа, то есть ( a + 1) p ? Это число можно представить в виде следующего выражения:

( a + 1) p = ( a + 1) ( a + 1) ( a + 1) … ( a + 1).

Или, другими словами, необходимо перемножить p чисел ( a + 1). Такое вычисление может показаться страшно утомительным — особенно если p является очень большим простым числом. Однако из этого вычисления можно кое-что установить.

Давайте, например, рассмотрим его для простого числа p = 5. В результате перемножения получаем:

( a + 1) 5 = ( a + 1) ( a + 1) ( a + 1) ( a + 1) ( a + 1) = a 5 + 1 + 5 a 4 + 10 a ³ + 10 a ² + 5 a .

Как мы приходим к такому результату? С первым слагаемым a 5 все ясно: все пять первых слагаемых a в скобках перемножаются между собой. Также все ясно со вторым слагаемым: все пять вторых слагаемых 1 в скобках тоже были перемножены между собой. Третье слагаемое 5 a 4получается так: из выражений в скобках берут четыре первых слагаемых a , одно второе слагаемое 1 и перемножают их между собой. Получается ровно пять возможностей выбора, откуда возникает множитель 5 перед степенью a 4. Точно так же можно объяснить, откуда берется последнее слагаемое 5 a . Четвертое слагаемое 10 a ³ получается так: из скобок выбирают три первых слагаемых a и два вторых слагаемых 1 и перемножают их. Сколько возможностей такого выбора? Для одного второго слагаемого 1 таких возможностей ровно пять, а для другого второго слагаемого 1 только четыре, ибо одно из чисел 1 уже было выбрано в качестве первого слагаемого 1. Всего это означает 5 × 4 = 20 возможных выборов. Впрочем, надо обратить внимание на то, что каждые два выбора из них дают одинаковые результаты, ибо для обоих выбранных чисел 1 совершенно безразлично, какое из них было «первым», а какое «вторым» из выбранных слагаемых. Число возможных перестановок двух выбранных чисел равно 1 × 2 = 2. На это число 2 надо разделить число 20, откуда получается множитель 10 перед степенью a ³. И наконец, пятое слагаемое 10 a ² получается следующим образом: из скобок выбирают два первых слагаемых a и три вторых слагаемых 1 и перемножают их всеми возможными способами. Сколько существует возможностей выбора? Для первого из двух слагаемых 1 таких возможностей, очевидно, пять, для следующего второго слагаемого 1 остается только четыре, а у третьего и последнего второго слагаемого 1 таких возможностей всего три. Это означает, что возможных вариантов перемножения будет 5 × 4 × 3 = 60. Надо, однако, учесть, что для каждого выбора в каждых шести выборах результат перемножения будет одним и тем же, ибо не важно, какое именно из трех чисел 1 было «первым», «вторым» или «третьим» выбрано вторым слагаемым 1. Число возможных перестановок из трех выбранных чисел равно 1 × 2 × 3 = 6. Надо разделить 60 на это число, и мы получим множитель 10 перед степенью a ².

Надо при этом заметить, что все множители 5, 10, 10 и 5 делятся на пять. Это связано с тем, что пять — простое число.

Теперь запишем в общем виде, как вычисляют выражения вида

( a + 1) p = ( a + 1) ( a + 1) ( a + 1)… ( a + 1).

Для начала надо перемножить между собой все слагаемые a . Это дает в результате a p . Вторым шагом является перемножение между собой всех слагаемых 1. Это дает в результате 1 p = 1. То есть:

( a + 1) p = ( a + 1) ( a + 1) ( a + 1)… ( a + 1) = a p + 1 + …

То, что здесь стыдливо обозначено точками …, — это все остальное, что получается от перемножения друг на друга всех слагаемых. В ходе такого перемножения будут получаться степени a p — 1, a p — 2, a p — 3, и вопрос заключается в том, насколько часто будет встречаться каждая из этих степеней. Например, степень a p — 1 получается оттого, что p — 1 первых слагаемых a перемножают с одним из всех вторых слагаемых 1. Всего возможностей для такого перемножения существует ровно p . Таким образом, степень a p — 1 появится на месте точек в виде pa p — 1. Или степень a p — 2 появляется в результате того, что p — 2 первых слагаемых a перемножаются с двумя вторыми слагаемыми. Сколько раз эта степень встретится в результатах перемножения? Для одного из обоих вторых слагаемых 1 существует p возможностей выбора, а для другого второго слагаемого таких возможностей остается уже p — 1. Всего таких возможностей, следовательно, будет p × ( p — 1). Однако это выражение надо разделить на произведение 1 × 2, потому что совершенно несущественно, какое из двух слагаемых 1 было выбрано первым, а какое — вторым. Таким образом, степень a p — 2встречается среди слагаемых, замененных точками,

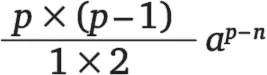
раз. В общем виде можно представить, что степень a p — n возникает в результате того, что p — n первых слагаемых a перемножают в точности с n вторых слагаемых 1. Сколько раз встретится в окончательном результате перемножения степень a p — n ? Для первого из n вторых слагаемых существует ровно p возможных выборов, для второго слагаемого 1 существует только p – 1 возможных выборов, и так далее, вплоть до n -го слагаемого 1, для которого число возможных выборов равно p — n + 1. В результате число возможных выборов становится равно p × ( p — 1) × … × ( p – n + 1). Это число, однако, надо разделить на произведение 1 × 2 × 3 × … × n , ибо какое из n слагаемых 1 будет выбрано в качестве первого, второго, …, n -го, представляется несущественным. Таким образом, степень a p — n встретится на месте точек