Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

Во время суда над Салли Кларк противоречивые доказательства мешали присяжным принять однозначное решение. Салли твердила, что она не убивала своих детей. Патологоанатом Министерства внутренних дел и свидетель-эксперт обвинения, доктор Алан Уильямс, утверждал обратное. Медицинская экспертиза, которую он представил, была запутанной и слишком сложной для присяжных. Во время подготовки к судебному процессу независимые эксперты легко дискредитировали разрывы в тканях мозга, повреждения позвоночника и кровоизлияния в сетчатку, которые Уильямс первоначально «обнаружил» при вскрытии Гарри. В результате обвинение изменило позицию и попыталось убедить присяжных в том, что Гарри задушили, а не затрясли до смерти, как утверждалось первоначально. Даже Уильямс передумал. Экспертно-медицинские заключения были исключительно туманны и неоднозначны.

Ожесточенная борьба между защитой и обвинением вокруг косвенных улик, связанных с этими двумя смертями, запутала ситуацию еще сильнее. Обвинение изображало Салли тщеславной и эгоистичной карьеристкой, раздраженной тем, как изменились ее образ жизни и ее тело после рождения детей. Женщиной, которая так отчаянно стремилась вернуться к своей прежней, бездетной жизни, что убила своих малышей. Почему же тогда, возражала защита, она так быстро родила второго ребенка? И почему она вновь забеременела и родила третьего, пока шла подготовка к суду? Защита утверждала, что Салли была явно опечалена смертью своего первого сына. Сторона обвинения пыталась использовать аргумент в свою пользу, намекая, что в таком демонстративном горе было что-то подозрительное. Врач, впервые увидевший Кристофера, когда тот приехал в больницу, возразил, что в отчаянии Салли не было ничего необычного – это естественная реакция на потерю первенца. Стороны перебрасывались аргументами, как воланчиком в бадминтоне, и у присяжных голова шла кругом.

Среди этой путаницы в дело вступил свидетель-эксперт, профессор сэр Рой Мидоу. В то время как патологи спорили о степени «легочного кровотечения» и «субдуральных гематом», Мидоу вел присяжных от подводных скал замешательства к спокойным водам вердикта, на яркий свет маяка статистики. Он оперировал единственным показателем, постулировавшим, что вероятность синдрома внезапной детской смерти (СВДС, который также часто называют смертью в колыбели) у двух подряд детей из обеспеченной семьи составляет 1 на 73 миллиона. Для многих присяжных это оказалась самая важная информация, которую они извлекли из процесса: 73 миллиона было слишком большим числом, чтобы его игнорировать.

В 1989 году под редакцией Мидоу, уже тогда известного британского педиатра, вышла книга «Азбука жестокого обращения с детьми». В ней был постулат, который позже назвали «законом Мидоу»: «Одна внезапная детская смерть – трагедия, две – уже повод для подозрений, а три – убийство, пока не будет доказано обратное» [88] Meadow, R. (Ed.) (1989). ABC of Child Abuse (First edition). British Medical Journal Publishing Group. . Однако эта бойкая сентенция основана на фундаментальном непонимании природы вероятности. С помощью такого же ложного представления о вероятности – разнице между зависимыми и независимыми событиями – Мидоу ввел в заблуждение и присяжных в случае с Салли Кларк.

Два события считаются зависимыми, если знание о том, что произошло одно из них, влияет на вероятность происхождения другого. В противном случае они независимы. Для расчета вероятности того, что произойдет комбинация нескольких событий, обычно перемножают вероятности происхождения каждого из них. Так, шанс, что случайно выбранный из населения человек является женщиной, составляет ½. Как показано в табл. 3, из 1000 человек в среднем 500 будут женщинами. Вероятность того, что у случайно выбранного человека из числа всего населения коэффициент IQ будет больше 110 баллов, составляет ¼ (таким образом, из 1000 человек такой результат покажут 250 – см. таблицу 3). Чтобы выяснить вероятность того, что произвольно выбранная женщина обладает IQ выше 110, мы перемножаем вероятности ½ и ¼, что дает вероятность 1/8 (и соответствует количеству 125 (1000/8) человек в подгруппе женщин с высоким IQ в табл. 3). Это прекрасный пример такой методологии, поскольку показатель IQ и половая принадлежность абсолютно независимы: наличие определенного IQ ничего не говорит о вашем поле, а принадлежность к определенному полу ничего не говорит о вашем IQ.

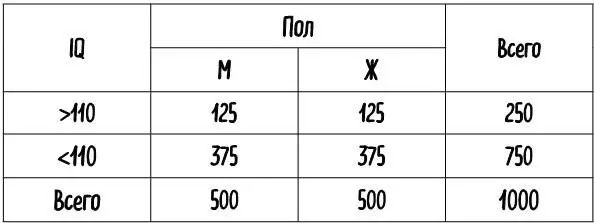
Табл. 3. Распределение 1000 человек по показателю IQ и половой принадлежности

Распространенность аутизма в Великобритании составляет примерно 1 на 100 [89] Brugha, T., Cooper, S., McManus, S., Purdon, S., Smith, J., Scott, F., Tyrer, F. (2012). Estimating the Prevalence of Autism Spectrum Conditions in Adults – Extending the 2007 Adult Psychiatric Morbidity Survey – NHS Digital. , или, соответственно, 10 на 1000. Действуя по описанной выше логике, можно предположить, что для определения вероятности того, что произвольно взятая женщина будет страдать аутизмом, надо просто перемножить две вероятности (1/2 и 1/100), что в итоге даст 1/200, то есть распространенность составит 5 случаев на 1000 человек. Однако аутизм и пол не являются независимыми вероятностями. При анализе 1000 случайно выбранных людей в популяции, как показано в табл. 4, мы увидим, что вероятность аутизма у мужчин в четыре раза выше (8 на 500), чем у женщин (2 на 500). Только 1 из 5 человек, страдающих аутизмом, будет женщиной [90] Ehlers, S., & Gillberg, C. (1993). The Epidemiology of Asperger Syndrome. Journal of Child Psychology and Psychiatry, 34 (8), 1327–50. https://doi.org/10.1111/j.1469–7610.1993.tb02094.x . Нам нужна эта дополнительная информация, чтобы корректно вычислить вероятность того, что случайно выбранный человек в популяции будет и женщиной, и аутистом одновременно. Верное значение этой вероятности составит 2/1000, а не 5/1000, что мы получили бы, ошибочно предположив независимость отдельных вероятностей. Пример демонстрирует, как легко совершить серьезные ошибки, опираясь на неверные предположения о независимости событий.

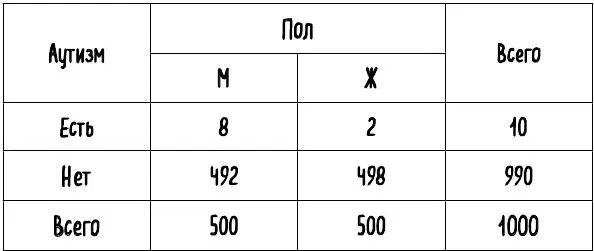
Табл. 4. Распределение 1000 человек по половой принадлежности и наличию аутизма

В своих показаниях Мидоу рассматривал смерти детей Салли Кларк в результате СВДС как отдельные вероятностные события. В вычислениях он опирался на данные тогда еще не опубликованного доклада о синдроме внезапной детской смерти, для которого ему предложили написать предисловие [91] Fleming, P. J., Blair, P. S. P., Bacon, C., & Berry, P. J. (2000). Sudden unexpected deaths in infancy: the CESDI SUDI studies 1993–1996. The Stationery Office. Leach, C. E. A., Blair, P. S., Fleming, P. J., Smith, I. J., Platt, M. W., Berry, P. J., Group, the C. S. R. (1999). Epidemiology of SIDS and explained sudden infant deaths. Pediatrics, 104 (4), e43. . В докладе на материале английской статистики было изучено 363 случая СВДС, пришедшихся на общее число в 473 родившихся живыми младенцев за трехлетний период. Наряду с общей частотой внезапной детской смертности по всему населению доклад представил распределение данных по возрасту матерей, доходам домохозяйств, а также по тому, курил ли кто-либо из членов семьи. В обеспеченных некурящих семьях с матерью старше 26 лет – таких как семья Кларк – на каждые 8543 живорожденных приходился всего один случай СВДС.