Кит Йейтс - Математика жизни и смерти. 7 математических принципов, формирующих нашу жизнь

Один из видов экологической ошибки – это поверхностное допущение, что обо всей разнообразной популяции можно судить по одному статистическому параметру. Так, в Великобритании в 2010 году средняя ожидаемая продолжительность жизни женщин составляла 83 года, а мужчин – всего 79 лет. Общая ожидаемая продолжительность жизни населения, таким образом, составила 81 год. Но утверждение, что любая случайно выбранная женщина будет жить дольше, чем любой случайно выбранный мужчина, сделанное на основании того, что средняя ожидаемая продолжительность жизни у женщин выше, чем у мужчин, и будет типичным примером экологической ошибки. Этот тип ошибки имеет собственное (очень подходящее) название – абстрактное обобщение. Другая распространенная экологическая ошибка – утверждение, что «мы все живем дольше», основанное на поверхностной интерпретации данных об увеличении общей продолжительности жизни. Им часто злоупотребляют ленивые журналисты. Говорить, что все будут жить дольше, чем ожидалось прежде, нельзя. Очевидно, что в лучшем случае это наивные предположения.

Однако экологические ошибки могут быть и менее очевидными. Как ни удивительно, при средней продолжительности жизни в 78,8 года большинство британских мужчин проживет дольше, чем при общей продолжительности жизни населения 81 год. На первый взгляд утверждение кажется противоречивым, но на самом деле это связано со спецификой использования статистических методов для обобщения данных. Небольшое, но значимое количество людей, умирающих молодыми, снижает средний возраст смерти (обычно за общую продолжительность жизни принимают сумму возрастов всех людей на момент смерти каждого, деленную на общее число людей). Как ни странно, эти ранние смерти опускают среднее значение продолжительности жизни намного ниже медианного (возраста, который не переживают столько же людей, сколько и переживают его). Медианный возраст смерти мужчин в Великобритании составляет 82 года, то есть до этих лет доживет как минимум половина из них. В данном случае представленная сводная статистика – средняя продолжительность жизни в 78,8 года – является исключительно недостоверной характеристикой мужской половины британцев.

Гауссова кривая, или кривая нормального распределения, с помощью которой можно описывать самые разные обыденные наборы данных – от роста до показателей IQ, – выглядит как гармоничная симметричная кривая, в которой половина данных лежит на одной стороне среднего значения, а половина – на другой. Это означает, что среднее и медианное – среднее значение распределения данных – значение характеристик, которые подчиняются этому распределению, склонны совпадать. Привыкнув к тому, что эту замечательную кривую можно использовать для описания реальных событий и явлений, многие из нас предполагают, что понятие «среднего» является хорошим маркером «середины» набора данных. Столкновение же с распределениями, где среднее значение не совпадает с медианным, может нас ошарашить. Распределение возраста смерти британских мужчин, показанное на рис. 11, явно далеко от симметрии. Поэтому подобные распределения обычно называют «смещенными» или «асимметричными».

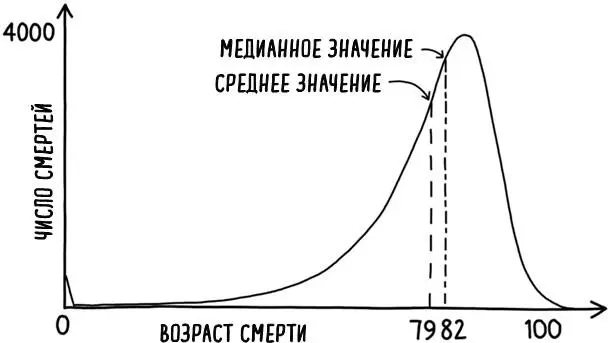
Рис. 11. Возрастная зависимость числа смертей в год у мужчин в Великобритании следует искаженному распределению. Средний возраст смерти составляет чуть менее 79 лет, в то время как медианный возраст – 82 года

Как мы видели в предыдущей главе (где познакомились с медианой, обсуждая способы предотвратить ложные срабатывания сигнала тревоги), распределение доходов домохозяйств – это еще один статистический показатель, медианное значение которого сильно отличается от среднестатистического. Распределение доходов домохозяйств в Великобритании, показанное на рис. 4, также асимметрично; та кривая очень напоминает изломанную и зеркально отображенную версию кривой на рис. 11. Большинство домохозяйств Великобритании имеют низкий располагаемый доход, но есть небольшое, но статистически значимое число богатых, которое искажает симметрию распределения. В 2014 году недельные доходы двух третей британцев были ниже «среднего» уровня.

Поначалу еще более удивительным примером кажется старая загадка: «Каков шанс на то, что у следующего человека, которого вы встретите на улице, ног будет больше, чем в среднем у людей?» Ответ: «Почти наверняка». Соль в том, что одноногих или вовсе безногих калек очень немного, но они и обеспечивают некоторое снижение среднего количества ног в пересчете на все население. Так что каждый, у кого две ноги, имеет больше ног, чем все население в среднем. Этот пример показывает, насколько смехотворны попытки оценивать индивидуальные качества, исходя из усредненных показателей по всей популяции.

Очевидно, что использование некорректного усреднения для описания популяции может привести к экологическим ошибкам. Еще один тип экологической ошибки, известный как парадокс Симпсона, возникает, когда мы пытаемся взять среднее значение из двух и более разнородных групп данных. Парадокс Симпсона проявляется в самых разных областях – от оценки состояния экономики [94] Ma, Y. Z. (2015). Simpson’s paradox in GDP and per capita GDP growths. Empirical Economics, 49 (4), 1301–15. https://doi.org/ 10.1007/s00181-015-0921-3 до интерпретации социально-демографических электоральных профилей [95] Nurmi, H. (1998). Voting paradoxes and referenda. Social Choice and Welfare, 15 (3), 333–50. https://doi.org/10.1007/s003550050109 и, что, возможно, наиболее важно, в разработке лекарств [96] Abramson, N. S., Kelsey, S. F., Safar, P., & Sutton-Tyrrell, K. (1992). Simpson’s paradox and clinical trials: What you find is not necessarily what you prove. Annals of Emergency Medicine, 21 (12), 1480–82. https://doi.org/10.1016/S0196-0644 (05) 80066-6 . Представьте себе, например, что мы отвечаем за контролируемое испытание нового препарата для снижения давления «Фантастикол». На исследование записалось 2000 добровольцев обоих полов, причем количество мужчин и женщин получилось равным. В целях контроля мы разделили их на две группы по 1000 человек. Пациенты в группе А получат «Фантастикол», а пациенты в группе Б – плацебо. В конце исследования выяснилось, что у 56 % (560 из 1000) человек, получавших препарат, артериальное давление снизилось, а в группе получавших плацебо этот эффект наблюдался только у 35 % (350 из 1000) добровольцев (см. таблицу 5). Похоже, что «Фантастикол» действительно работает.

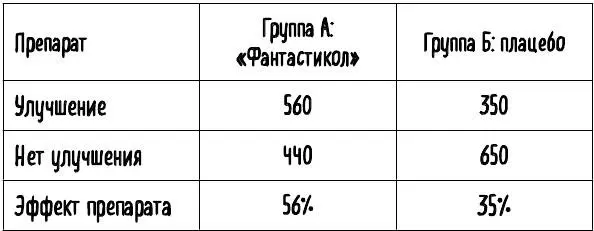
Табл. 5. «Фантастикол», похоже, оказывает в целом более существенный благоприятный эффект, чем плацебо

Для правильной адресации препарата важно знать особенности его воздействия с учетом половой принадлежности пациента. Следовательно, нам нужно понять, как наш препарат действует на мужчин и женщин по отдельности, поэтому мы перераспределяем наши статистические данные соответственно. Эта более подробная разбивка приведена в табл. 6. Анализ результатов оказывается несколько неожиданным. У мужчин из группы Б, принимавших плацебо, артериальное давление понизилось у 25 % (200 из 800 в группе Б), а вот у мужчин из группы А, принимавших «Фантастикол», такой же благотворный эффект наблюдался лишь в 20 % случаев (40 из 200). Среди женщин очевидна та же тенденция: в группе Б давление понизилось в 75 % случаях (150 из 200), а в группе А – только в 65 % случаев (520 из 800). Для обоих полов доля тех, на ком плацебо сказался благотворнее, чем «Фантастикол», оказывается выше. В этом свете новый препарат уже кажется менее эффективным, чем плацебо. Как может быть, что при разбиении данных на группы и их стратификации исследование рассказывает одну историю, а при объединении групп – противоположную, и какая из этих историй правдива?