Александр Львовский - Отличная квантовая механика

a) Покажите, что невозможно построить устройство, которое всегда достоверно определяло бы состояние системы.

b) * Покажите, что можно сконструировать измерительное устройство, которое будет выдавать, с некоторой вероятностью, результаты трех типов: «определенно | a ⟩», «определенно | b ⟩» и «не уверен», причем результаты первых двух типов всегда будут верными.

Подсказка:попробуйте использовать неполяризующий светоделитель — оптический элемент, который случайным образом либо пропускает, либо отражает фотон вне зависимости от его поляризации.

Рассмотрим эксперимент, показанный на рис. 1.3. Единичный фотон, находившийся первоначально в диагонально поляризованном состоянии 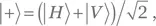попадает в устройство, известное как интерферометр [19] Конкретнее, интерферометр Маха — Цендера. . Сначала PBS пропускает горизонтальный компонент состояния и отражает вертикальный. Затем отраженный компонент проходит через варьируемую линию задержки [20] Считаем, что линия задержки много короче, чем длина светового импульса, так что изменение задержки не влияет на видность интерференции. , и оба компонента вновь соединяются при помощи еще одного PBS. После этого состояние на выходе интерферометра подвергается измерению в диагональном базисе.

Линия задержки вводит разницу между оптической длиной пути вертикального и горизонтального компонентов. Если длина этой линии равна l , то вертикальный компонент получит сдвиг фазы на ϕ = kl по отношению к горизонтальному, где k = 2π/λ есть волновое число. В результате фотон, выходя из интерферометра, будет в состоянии

Мы изучили измерение этого состояния в упр. 1.14 и выяснили, что вероятности срабатывания детекторов «+» и «−» составляют 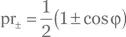соответственно. При изменении длины линии задержки вероятности меняются синусоидально. Иными словами, мы увидим интерференционные полосы — такие же, какие в таком оптическом устройстве образовала бы макроскопическая волна.

Что в этом выводе поистине замечательно (и, разумеется, целиком и полностью подтверждено экспериментально), так это то, что интерференционные полосы порождает один-единственный фотон. Это решительно противоречит нашим интуитивным представлениям. Действительно, в классическом эксперименте интерференция возникает потому, что две волны, проходящие по двум путям интерферометра, получают разные фазы и затем складываются когерентно на фотодетекторах. Но в нашем эксперименте присутствует всего один фотон! Фотон — неделимая элементарная частица света, поэтому он не может расщепиться [21] Позже мы увидим, что на самом деле фотон может расщепиться на два фотона с меньшей энергией при нелинейном оптическом явлении, известном как параметрическое рассеяние. Однако этот довольно экзотический эффект возникает с низкой вероятностью и только в особых условиях. Наш интерферометр не содержит нелинейных оптических элементов, так что параметрическое рассеяние здесь ни при чем. в интерферометре и породить две волны, необходимые для образования интерференционных полос. Он должен двигаться в одиночестве либо по верхнему, либо по нижнему пути интерферометра — но не по двум путям одновременно.

Эти разумные и интуитивно понятные доводы противоречат и нашим расчетам, и экспериментальным наблюдениям. Как можно это объяснить?

Фотон, попадающий в интерферометр, находится в суперпозиции состояний вертикальной и горизонтальной поляризации. После первого PBS он по-прежнему находится в состоянии суперпозиции — но теперь это также суперпозиция верхнего и нижнего путей интерферометра. После воссоединения путей она вновь превращается в суперпозицию состояний поляризации — но уже с фазовым сдвигом у одного из ее компонентов. Именно эти два компонента суперпозиции играют здесь роль двух волн из классического эксперимента и интерферируют друг с другом. Так проявляется корпускулярно-волновой дуализм (wave-particle duality) квантовых частиц [22] Именно поэтому, вероятно, популярные книги по квантовой механике любят описывать состояния суперпозиции как состояния, в которых «объект находится в двух разных местах в одно и то же время». .

Получается, что в определенном смысле фотон все-таки расщепляется между двумя каналами интерферометра. Однако такое волноподобное поведение возможно только в том случае, если компоненты остаются в состоянии суперпозиции. Чтобы это проиллюстрировать, предположим, что в обоих каналах интерферометра мы размещаем детекторы, способные регистрировать фотоны, не разрушая их. Всякий раз, когда какой-нибудь фотон попадает в интерферометр, один из этих детекторов срабатывает и показывает нам, по верхнему или по нижнему пути прошел фотон. Таким способом, как сказали бы отцы-основатели квантовой механики, мы получаем о фотоне информацию Welcher Weg [23] «Который путь» (нем.). .

Получение информации Welcher Weg означает измерение положения фотона. В предыдущем разделе мы узнали, что такое измерение схлопывает состояние суперпозиции и превращает его, в зависимости от результата, либо в фотон, находящийся на верхнем, либо в фотон, находящийся на нижнем пути интерферометра. Глядя на детектор Welcher Weg , наблюдатель может точно сказать, в каком состоянии — горизонтальном или вертикальном — фотон выйдет из интерферометра. Так или иначе, последующее измерение этого фотона в диагональном базисе выдаст тот или другой результат с вероятностью 1/2 независимо от разности хода. Таким образом измерение Welcher Weg разрушает волновые свойства фотона и заставляет его вести себя как частица.

Отступление 1.4.Квантовая инспекция военной техники

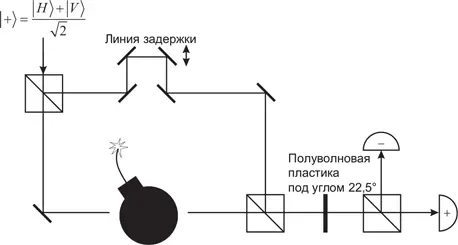
Вот любопытный парадокс, связанный с экспериментом по однофотонной интерференции, обсуждающийся в разд. 1.5 [24] A. C. Elitzur, L. Vaidman, Quantum mechanical interaction-free measurements , Foundations of Physics 23 , 987 (1993). . Пусть имеется бомба, оборудованная датчиком фотонов и настроенная так, что взорвется, даже если датчик провзаимодействует с одним-единственным фотоном. Можем ли мы обнаружить присутствие бомбы в одном из каналов нашего интерферометра, не подорвав ее при этом?