Александр Львовский - Отличная квантовая механика

Здесь есть сложный момент, который следует прояснить. Множество углов поляризации линейно поляризованных фотонов — континуум. Но в случае одномерного движения частицы, о котором говорилось в предыдущем разделе, множество позиционных состояний — также континуум. Почему же мы говорим, что одно из этих гильбертовых пространств имеет размерность два, а другое — бесконечность?

Разница в том, что линейно поляризованные состояния могут быть записаны в виде (1.2), т. е. в виде суперпозиции других линейно поляризованных состояний. Если мы поместим поляризующий светоделитель (разд. В.2), пропускающий только горизонтально поляризованные фотоны, на пути диагонально поляризованной волны, часть ее пройдет сквозь светоделитель. Это означает, что диагонально поляризованный фотон может быть обнаружен в горизонтальном поляризационном состоянии.

Состояния же, связанные с разными положениями в пространстве, напротив, все ортогональны: частицу, приготовленную в состоянии | x = 3 м⟩, невозможно обнаружить в точке x = 4 м. Также невозможно записать позиционное состояние в виде суперпозиции других позиционных состояний. Это значит, что соответствующее гильбертово пространство должно иметь намного более широкий базис, чем гильбертово пространство поляризационных состояний.

Для классической волны (1.1) сдвиг фаз одновременно горизонтального и вертикального компонентов на равную величину (т. е. ϕ H→ ϕ H+ ϕ 0, ϕ V→ ϕ V+ ϕ 0, что эквивалентно умножению правой части на 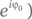не меняет ее поляризации.

Аналогичное правило применимо и к квантовым состояниям. Умножение вектора состояния на eiϕ не меняет физической природы состояния. К примеру, | V ⟩, i| V ⟩ и —| V ⟩ представляют один и тот же физический объект, как и, скажем, 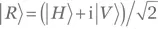и 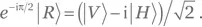По этой причине мы на время пренебрежем множителем e−iωt в (1.2).

Мы называем комплексную величину eiϕ с действительным ϕ фазовым множителем . Умножение квантового состояния на фазовый множитель называется применением фазового сдвига на ϕ. Соответственно мы говорим, что применение фазового сдвига к квантовому состоянию не меняет его физических свойств. Как мы увидим в следующем разделе, это правило оказывается весьма общим: оно выполняется для всех физических систем, не только для электромагнитных волн. Разумеется, фазовый сдвиг должен быть глобальной природы (overall phase shift): если мы применим его только к части состояния, это состояние изменится. Например, если мы применим фазовый сдвиг на π/2 к вертикальному компоненту поляризованного под +45° фотона, 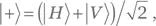то получим 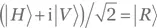— фотон с правой круговой поляризацией, т. е. физически отличный от первоначального объекта.

Поляризация фотона — это реализация квантового бита (кубита) . Данный термин используется для обозначения любой физической системы, гильбертово пространство которой двумерно, в контексте рассмотрения этой системы как носителя информации. Кубит — базовая единица квантовой информации, по аналогии с битом — единицей информации в классических компьютерах. В противоположность последнему квантовый бит может находиться не только в одном из двух базовых состояний, но и в их суперпозиции. Это открывает для нас множество новых технологических возможностей, которые мы будем обсуждать на протяжении всей книги.

Второй постулат относится к квантовым измерениям , т. е. к экспериментам, цель которых — получить информацию о квантовом состоянии некоторой системы. В классической, макроскопической физике измерения больше вопрос технологии, чем фундаментальной науки. Дело в том, что там мы можем точно измерить состояние и эволюцию системы, не потревожив ее. Так, футбольный мяч не полетит разными способами в зависимости от того, пуст стадион или заполнен до отказа восторженными болельщиками, — следовательно, нам не нужно знать, каким методом фиксируют траекторию мяча, чтобы изучить законы его движения.

В квантовом мире ситуация выглядит иначе: мы велики, а те объекты, которые мы хотим измерить, малы. Поэтому любое измерение, скорее всего, изменит квантовое состояние нашей системы. В более общем плане можно сказать, что квантовые измерения — это события, при которых состояние микроскопического квантового объекта влияет на состояние макроскопического прибора. Таким образом, измерение пересекает границу между квантовым и классическим царствами физики. А как мы знаем, законы, управляющие ими, сильно различаются между собой. Чтобы получить цельную картину мира, нам необходимо понять, когда и как происходит переход между этими двумя «юрисдикциями».

Далее, явления, при которых квантовое состояние чего-то микроскопического влияет на что-то макроскопическое, не ограничены стенами лабораторий. К ним относятся самые разные события — от термодинамических фазовых переходов и лазерной генерации до ураганов, рождения черных дыр и, возможно, рождения самой Вселенной. Физика подобных явлений аналогична физике квантовых измерений. Из этого следует, что разобраться в этой физике необходимо для понимания природы окружающего нас мира.

Основные принципы постулата об измерениях можно вывести интуитивно. Предположим, что фотон в состоянии (1.2) попадает в поляризующий светоделитель (PBS) — оптический элемент, который пропускает горизонтально поляризованный свет, но отражает вертикально поляризованный (рис. 1.2 a). Что произойдет с этим фотоном? Если бы мы имели дело с классической волной (1.1), то сказали бы, что она разделится: часть ее пройдет сквозь PBS, а остальное отразится. Доли энергии, попадающие в прямой и отраженный каналы, были бы пропорциональны 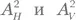соответственно. Но фотон — это наименьшая порция энергии света, и его невозможно поделить на части.

Мы подошли к очевидному противоречию. Мы знаем, с одной стороны, что классическая волна, состоящая из фотонов, делится на части. С другой — что каждый отдельный фотон неделим. Как могут два этих требования выполняться одновременно?

Представляется, что единственный способ разрешить данный парадокс состоит в том, чтобы постулировать, что результат в таком случае будет случайным : фотон пройдет через PBS с вероятностью 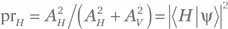и отразится с вероятностью 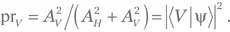Таким образом, если на PBS попадет большое число N фотонов, то численное соотношение пропущенной и отраженной энергий составит 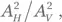как и ожидалось в классическом случае (см. разд. В.2). И при этом ни один индивидуальный фотон не придется делить на части.