Александр Львовский - Отличная квантовая механика

Предположим, что мы в состоянии выделить единичную частицу света — фотон — из поляризованной волны. Фотон — микроскопический объект, поэтому рассматривать его следует в рамках квантовой механики. Начнем с того, что определим связанное с ним гильбертово пространство. Для начала отметим, что горизонтально поляризованное состояние фотона, которое мы обозначим | H ⟩, несовместимо с его вертикально поляризованным состоянием | V ⟩: фотон | H ⟩ невозможно обнаружить в состоянии | V ⟩. То есть если мы приготовим горизонтально поляризованный фотон и прогоним его через поляризующий светоделитель (PBS, polarizing beam splitter ) — оптический элемент, описанный в разд. В.2, то данный фотон во всех случаях будет проходить насквозь, а отражаться не будет никогда. Это означает, что состояния | H ⟩ и | V ⟩ ортогональны.

Мы постулируем, что световая волна, электрическое поле которой задано в виде функции координаты и времени [см. (В.2)]

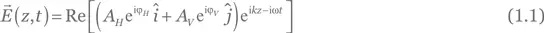
(с действительными A H,Vи ϕ H,V), состоит из фотонов в состоянии [7] Может показаться удивительным, что уравнение (1.2) не несет никакой информации о координате фотона по оси z . Причина в том, что этот фотон, будучи квантовой частицей, размазан в пространстве и времени. К факторам, влияющим на степень размазанности, относятся, в частности, характеристики источника, а также «объем квантования», выбранный для теоретического анализа. В случае лазерного луча длина фотона ограничивается длиной когерентности лазера, которая может составлять не один километр. В данной книге мы, как правило, будем считать, что фотоны размазаны на расстояние, намного превышающее размер любого прибора, и потому могут рассматриваться как бесконечно большие.

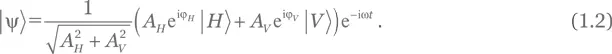
Отступление 1.1.Открытие фотона

В 1900 г. Макс Планк объяснил экспериментально наблюдаемый спектр излучения абсолютно черного тела, введя понятие кванта света, который мы сегодня знаем как фотон [8] M. Planck, Über das Gesetz der Energieverteilung im Normalspectrum , Annalen der Physik 4 , 553 (1901). . Он обнаружил, что хорошее совпадение теории и эксперимента можно получить, если считать, что энергия фотона пропорциональна частоте ω световой волны. Коэффициент пропорциональности ℏ = 1,05457148 × 10 −34получил название постоянной Планка.

В 1905 г. Альберт Эйнштейн еще раз подтвердил обоснованность формулы Планка

E = ℏω,

воспользовавшись ей для количественного объяснения экспериментальных результатов по фотоэлектрическому эффекту (более подробно см. отступление 4.6 [9] A. Einstein, Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt , Annalen der Physik 17 , 132 (1905). . Позже, в 1916 г., Эйнштейн сделал вывод, что, поскольку из классической электродинамики [10] Это явление выражается, в частности, в эффекте давления света, который экспериментально наблюдал Петр Лебедев в 1900 г. известно, что электромагнитный волновой пакет, несущий энергию E , несет также импульс p = E/c , это же соотношение должно выполняться и для фотонов. По формуле Планка он нашел [11] Выражение для импульса фотона можно получить также следующим образом. Воспользовавшись знаменитым уравнением Эйнштейна E = mc 2 и формулой Планка, мы можем рассчитать массу фотона M = ℏω/ c 2 . Фотон движется со скоростью света, следовательно, его импульс равен p = Mc = ℏω/ c . p = ℏω/ c . Выразив частоту волны через ее длину, он получил ω = 2πc/λ, а затем записал

p = 2πℏ/λ.

Артур Холли Комптон в 1923 г. использовал результаты Эйнштейна для теоретического объяснения собственных экспериментов, в которых он исследовал рассеяние рентгеновских лучей на свободных электронах [12] A. H. Compton, A Quantum Theory of the Scattering of X-Rays by Light Elements , Physical Review 21 483 (1923). . Рассматривая фотоны рентгеновского излучения как частицы высоких энергий, он применил законы сохранения энергии и импульса к столкновению между фотоном и электроном, чтобы рассчитать энергию рассеянных фотонов в зависимости от угла рассеяния. Затем он соотнес эту энергию с длиной волны — и получил теоретическое описание для своих экспериментальных данных. Увиденное им превосходное совпадение тех и других стало служить наглядным доказательством существования фотона.

Интересно отметить, что термина «фотон» в то время не существовало. Его ввел в 1926 г. специалист по физической химии Гильберт Льюис [13] G. N. Lewis, The conservation of photons , Nature 118 , 874 (1926). .

Например, если A H= A Vи ϕ H= ϕ V= 0, то соответствующая классическая волна выглядит как 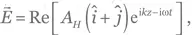т. е. линейно поляризована под углом +45°. Соответственно, состояние (где делитель 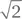связан с нормированием) обозначает единичный фотон с линейной поляризацией под +45°. В табл. 1.1 вы можете увидеть еще несколько примеров [14] Обсуждение договоренностей, принятых для состояний с круговой (циркулярной), поляризацией, см. в сноске 141. .

Из этого следует, что состояния | H ⟩ и | V ⟩ образуют в гильбертовом пространстве поляризационных состояний фотона ортонормальный базис — т. е. пространство двумерно. Действительно, прежде всего эти состояния ортогональны и потому линейно независимы (упр. A.17). Кроме того, любая поляризованная классическая волна может быть записана в виде (1.1), так что любое поляризационное состояние фотона тоже может быть записано аналогично (1.2), т. е. как линейная комбинация состояний | H ⟩ и | V ⟩. Мы будем называть базис {| H ⟩,| V ⟩} каноническим базисом нашего гильбертова пространства.

Упражнение 1.3.Покажите, что:

a) поляризационные состояния ±45° образуют ортонормальный базис;

b) правое и левое круговые поляризационные состояния образуют ортонормальный базис.

Упражнение 1.4.Разложите | H ⟩ и | V ⟩ по базисам {|+⟩,|—⟩} и {| R ⟩,| L ⟩}.

Упражнение 1.5.Разложите | a ⟩ = |+30°⟩ и | b ⟩ = |–30°⟩ по базисам {| H ⟩,| V ⟩}, {|+⟩,|—⟩} и {| R ⟩,| L ⟩}. Найдите скалярное произведение ⟨a|b⟩ во всех трех базисах, используя операцию перемножения матриц. Одинаковые ли получились результаты?