Александр Львовский - Отличная квантовая механика

Упражнение 1.8.Покажите, что:

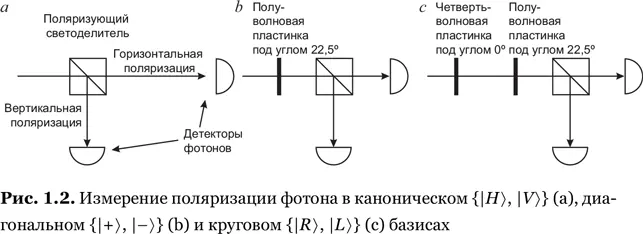
a) устройство на рис. 1.2b выполняет измерение поляризации фотона в диагональном (|±45º⟩) базисе;

b) устройство на рис. 1.2c выполняет это же измерение в круговом ({| R ⟩,| L ⟩}) базисе.

Подсказка:когда устройство, описанное в постулате об измерениях, измеряет одно из своих собственных базисных состояний |𝑣 i⟩, то результат измерения укажет на это состояние с вероятностью 1. Верно и обратное: если это устройство способно строго различить некий конкретный ортонормальный набор состояний, то мы можем сделать вывод, что этот набор является измерительным базисом данного устройства. Следовательно, чтобы выполнить это упражнение, достаточно показать, что базисные состояния [т. е. |±45º⟩ в варианте a) и | R ⟩, | L ⟩ в варианте b)] после PBS дадут щелчки на разных фотонных детекторах.

Отступление 1.3.Оптический стол

На этой фотографии вы видите типичный квантово-оптический эксперимент. Он выполняется на оптическом столе — массивной металлической плите, на которую устанавливаются различные оптические элементы, такие как линзы, зеркала, лазеры, кристаллы и детекторы. Лучи, как правило, проходят горизонтально, на одном уровне по всей длине стола.

Упражнение 1.9.§ Каждое из состояний | H ⟩, | V ⟩, |+⟩, |—⟩, | R ⟩, | L ⟩ измеряется в

a) каноническом,

b) диагональном,

c) круговом базисах.

Найдите вероятности возможных результатов для каждого случая.

Ответ:для каждого состояния, когда измерение производится в базисе, к которому принадлежит это состояние, вероятности составляют 0 и 1. Если же состояние не принадлежит к измерительному базису, то вероятность обоих результатов равняется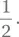

Упражнение 1.10.Предложите схему для квантового измерения в базисе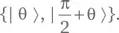

Упражнение 1.11.Предложите схему для квантового измерения в базисе {| R ⟩, | L ⟩}, в которой использовалась бы только одна волновая пластинка.

Упражнение 1.12.Рассмотрим фотон, который находится в состоянии не суперпозиции, а случайной статистической смеси , или ансамбля [17] Такие смешанные состояния не являются элементами квантового гильбертова пространства. Подробнее об этом см. подразд. 2.2.4. (statistical mixture/ensemble): либо | H ⟩ с вероятностью 1/2, либо | V ⟩ с вероятностью 1/2. Поляризация этого фотона измеряется в:

a) каноническом,

b) диагональном,

c) круговом базисах.

Найдите вероятности возможных результатов для каждого случая.

Упражнение 1.13.Фотон приготовлен с линейной поляризацией 30º к горизонтали. Найдите вероятность каждого результата, если его поляризация измеряется в:

a) каноническом,

b) диагональном и

c) круговом базисах.

Упражнение 1.14.Фотон в состоянии измеряется в диагональном базисе. Найдите вероятность каждого результата как функцию от ϕ.

Это упражнение, так же как и упр. 1.7, еще раз демонстрирует важную разницу между фазовым множителем, примененным к части квантового состояния или к квантовому состоянию целиком. В первом случае добавочная фаза влияет на измеряемые свойства объекта, во втором — нет.

Хотя одиночное измерение дает нам некоторую информацию о начальном состоянии квантовой системы, информация эта очень ограничена. Предположим, например, что мы измерили фотон в каноническом базисе и обнаружили, что он прошел через PBS. Можем ли мы из этого сделать вывод, что первоначальный фотон находился в состоянии | H ⟩? Нет, не можем. Он мог находиться в любом состоянии ψ H| H ⟩ + ψ V| V ⟩; коль скоро ψ H≠ 0, существует некоторая вероятность получения щелчка в пропускающем канале. Поэтому единственное, что мы узнаем из данного измерения, — это то, что фотон не был вертикально поляризован.

Теперь предположим, что мы провели одно и то же измерение неоднократно, каждый раз приготавливая наш фотон в одинаковом состоянии [18] Хотя мы не знаем, каково это состояние, мы можем многократно приготавливать фотон в одном и том же состоянии путем сохранения постоянных условий эксперимента. . Теперь мы знаем намного больше! Мы знаем, сколько щелчков получено нами от «горизонтального» детектора, а сколько — от «вертикального», т. е. у нас появилась статистика измерений . По этим данным мы можем рассчитать, с некоторой ошибкой, pr H= |ψ H| 2и pr V= |ψ V| 2, т. е. узнать кое-что об абсолютных величинах компонентов состояния. Но и ψ H, и ψ V— комплексные числа, и их аргументы (углы на комплексной плоскости) по-прежнему неизвестны. К примеру, если мы наблюдаем pr H= pr V= 1/2, то состояние |ψ⟩ может быть или | R ⟩, или | L ⟩, или |+⟩, или |—⟩, или еще каким-нибудь из множества вариантов. Что нам с этим делать?

Как видно из следующего упражнения, надлежит провести дополнительные серии измерений в других базисах. Полученная статистика даст новые уравнения, которые можно решить и найти ψ Hи ψ Vс точностью до неопределенности, связанной с общим фазовым множителем.

Упражнение 1.15.Предположим, что множественные измерения поляризации фотонов, идентично приготовленных в состоянии |ψ⟩, проводятся в каноническом, диагональном и круговом базисах и при этом определяются все шесть соответствующих вероятностей (pr H, pr V, pr +, pr —, pr R, pr L). Покажите, что этой информации достаточно, чтобы полностью определить |ψ⟩ и выразить его разложение в каноническом базисе через pr H, pr +и pr R. Приведите пример, показывающий, что измерений только в каноническом и диагональном базисах для этого было бы недостаточно, — т. е. найдите два различных состояния, которые дадут одинаковые pr Hи pr +.

Метод получения полной информации о квантовом состоянии путем проведения серий измерений в нескольких разных базисах на множестве идентичных копий измеряемого состояния называется томографией квантового состояния (quantum state tomography). Его можно обобщить на другие квантовые системы, включая системы более высокой размерности. Мы подробнее поговорим о квантовой томографии в конце основного текста (разд. 5.7).

Упражнение 1.16.Предположим, вам дан единственный экземпляр квантовой системы, находящейся в одном из двух неортогональных состояний | a ⟩ и | b ⟩. Вам известно, что это за состояния, но вы не знаете, в каком именно из них находится система.