Александр Львовский - Отличная квантовая механика
- Название:Отличная квантовая механика
- Автор:
- Жанр:
- Издательство:Альпина нон-фикшн
- Год:2019
- Город:Москва
- ISBN:978-5-0013-9162-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Александр Львовский - Отличная квантовая механика краткое содержание
В книге применяется математически простая физическая система — поляризация фотонов — в качестве инструмента визуализации, что позволяет студенту увидеть запутанную красоту квантового мира с самых первых страниц. Формальные концепции квантовой физики проиллюстрированы примерами из современных экспериментальных исследований, таких как квантовые компьютеры, коммуникации, телепортация и нелокальность.
Материал книги успешно использовался в качестве основного учебного пособия в двухсеместровом курсе по квантовой механике для студентов-физиков. Однако потенциальный круг читателей много шире и охватывает как студентов и аспирантов, изучающих точные науки, так и всех интересующихся квантовой физикой и квантовыми технологиями. Математический аппарат, требующийся для понимания книги, не выходит за пределы курса технического вуза или математической школы.
Автор — профессор Оксфордского университета, экспериментатор с мировым именем в области квантовой оптики и квантовой информатики — применяет сократовскую педагогику: студенту предлагается самостоятельно разработать аппарат квантовой физики путем последовательного решения тщательно составленных задач. Подробные решения представлены во втором томе пособия.
Отличная квантовая механика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
129
Конечно, если квантовый процесс описывается оператором, тот должен быть не просто линейным, но также унитарным (см. разд. 1.10). Однако для данного упражнения этот факт не существенен.
130
На самом деле достаточно, чтобы набор 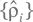 был остовным; ему не обязательно быть линейно независимым.
был остовным; ему не обязательно быть линейно независимым.
131
При n ≠ m это всего лишь формальные математические объекты, которые не соответствуют никаким физическим состояниям. Однако они удобны для тренировки интуиции.
132
Поле — это понятие из алгебры, обозначающее полное множество некоторых чисел. Примерами полей могут служить множества рациональных (ℚ), действительных (ℝ) и комплексных (ℂ) чисел. Квантовая механика обычно имеет дело с векторными пространствами над полем комплексных чисел.
133
Обратите внимание: в качестве альтернативной нотации для |zero⟩ мы иногда используем просто 0, но никогда не |0⟩.
134
То есть такая, в которой по крайней мере один из коэффициентов не равен нулю.
135
Мы используем символ ≃ вместо =, когда выражаем векторы и операторы в матричной форме, как в (A.2). Делается это для того, чтобы подчеркнуть разницу: левая часть (вектор) представляет собой абстрактный объект и не зависит от базиса, тогда как правая часть — это набор чисел, зависящий от выбора базиса {|𝑣i⟩}. Однако в литературе, как правило, для простоты используется знак равенства.
136
Отображение — это функция, которая устанавливает для каждого элемента | a ⟩ в 𝕍 уникальный «образ» Â | a ⟩.
137
ℂ 2есть линейное пространство столбцов 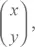 содержащих по два комплексных числа.
содержащих по два комплексных числа.
138
Это упрощенный вид формулы Бейкера — Хаусдорфа — Кэмпбелла. Полный вид этой формулы более сложен и выполняется в том числе для случая, когда 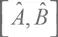 не коммутирует с
не коммутирует с 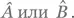
139
На протяжении всей книги я использую нижние индексы для обозначения дискретных вероятностей, таких как pri или 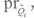 и скобки для обозначения непрерывных плотностей вероятности, к примеру pr( Q ).
и скобки для обозначения непрерывных плотностей вероятности, к примеру pr( Q ).
140
Строгая формулировка этого утверждения называется центральной предельной теоремой.
141
Определение того, какая из круговых поляризационных схем должна называться «левой», а какая «правой», — вопрос соглашения. Здесь мы следуем соглашению, принятому в квантовой оптике. В право-циркулярной схеме конец вектора электрического поля вращается по часовой стрелке, если смотреть «сзади» относительно волны (от источника). Однако вращение происходит против часовой стрелки, если смотреть «спереди», или в плоскости x-y с традиционной ориентацией осей. В пространстве эта траектория имеет вид левого винта.
142
Гладкой называется функция, имеющая производные всех конечных порядков.
143
Не существует общепринятой договоренности ни о том, где ставить минус в показателе комплексной экспоненты — в уравнении (Г.10) или (Г.21), ни о том, как распределить между ними множитель 1/2π. Для этой книги я выбрал договоренность по своему собственному вкусу.
144
Реальная скорость передачи секретного ключа несколько ниже из-за «наценки», связанной с усилением секретности.
145
Здесь мы пренебрегаем относительным сдвигом фазы, который PBS налагает на пары вертикальных и горизонтальных фотонов.
146
Строго говоря, решение для φ не определено, если либо ψ↑, либо ψ↓ обнуляется. Тем не менее эти случаи соответствуют уникальным блоховским векторам, указывающим на северный и южный полюса блоховской сферы соответственно.
147
В этих рассуждениях мы пренебрегаем соглашением о том, что полярный угол θ должен находиться в интервале от 0 до π. Если мы хотим учитывать это соглашение, нам следует переопределить полярные углы следующим образом. Обозначим θ′ = 4α mod π. Тогда 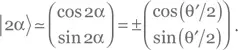 При 0 ≤ θ′ ≤ π это состояние соответствует блоховскому вектору с θ = θ′, φ = 0. При π < θ′ < 2π мы можем записать
При 0 ≤ θ′ ≤ π это состояние соответствует блоховскому вектору с θ = θ′, φ = 0. При π < θ′ < 2π мы можем записать 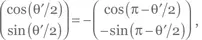 что соответствует блоховскому вектору с θ = 2π — θ′, φ = π. В обоих случаях θ ∈ [0, π].
что соответствует блоховскому вектору с θ = 2π — θ′, φ = π. В обоих случаях θ ∈ [0, π].
Этот более строгий подход дает нам то же самое геометрическое место на сфере Блоха, что и приведенный выше упрощенный.
148
Это соответствует географической широте π/2 — θ.
149
Обратите внимание на знак: фиктивное поле 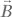 направлено вдоль отрицательной оси z при положительном Δ. Это означает, что при положительном Δ полярный угол вектора Блоха увеличивается со временем. Все происходит наоборот по отношению к упр. 4.62, a), где поле направлено вдоль положительного направления оси z, а полярный угол вектора Блоха со временем уменьшается.
направлено вдоль отрицательной оси z при положительном Δ. Это означает, что при положительном Δ полярный угол вектора Блоха увеличивается со временем. Все происходит наоборот по отношению к упр. 4.62, a), где поле направлено вдоль положительного направления оси z, а полярный угол вектора Блоха со временем уменьшается.
150
Конечно, эти векторы представляют собой просто наборы чисел, а не квантовые состояния.
151
Логарифм и квадратный корень — примеры многозначных функций, весьма распространенных в комплексном анализе.
Интервал:
Закладка:








