Александр Львовский - Отличная квантовая механика

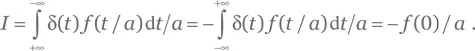
Два приведенных выше уравнения можно объединить, написав

Сравнив уравнения (Г.3) и (РГ.2), получаем:

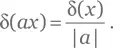
Решение для упражнения Г.3.Пусть dθ( x )/d x = α( x ). Рассмотрим интеграл

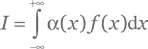
гладкой ограниченной функции 𝑓( x ). Интегрируя по частям, находим:

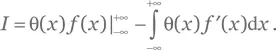
Первый член в этом выражении равен 𝑓(+∞). Второй член, согласно определению функции Хевисайда, равен

так что I = 𝑓(0). Таким образом, обобщенная функция α( x ) ведет себя в соответствии с определением (Г.3) дельта-функции; следовательно, она является дельта-функцией.

Решение для упражнения Г.4

где θ( x ) есть функция Хевисайда, и мы воспользовались формулой Ньютона — Лейбница.

Решение для упражнения Г.5

a) Это следует из определения (Г.10) преобразования Фурье при k = 0.

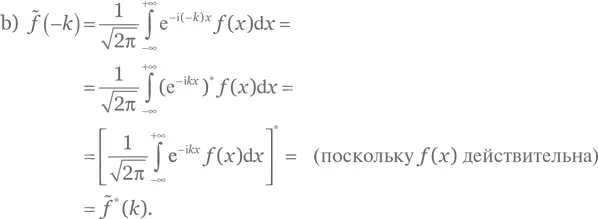
с) Вводим новую переменную интегрирования t = ax и действуем по аналогии с упр. Г.2, c).

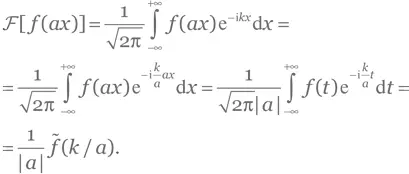
d) Заменим переменную интегрирования на t = x — a . Получаем:

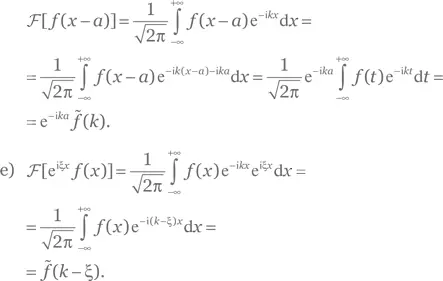
f) Воспользуемся интегрированием по частям и учтем, что 𝑓( x ) обнуляется на ±∞:

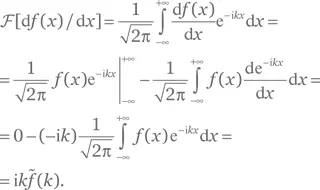
Решение для упражнения Г.6.Чтобы вычислить интеграл

выразим экспоненту в уравнении (РГ.3) как квадратичную функцию от x , а затем применим (Б.17):

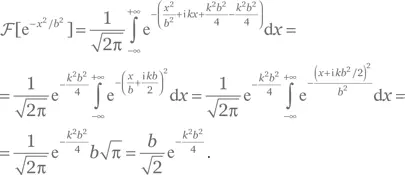
Решение для упражнения Г.7

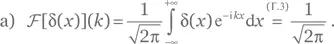
b) Приравняв d к 2/ b , мы можем переписать (Г.1) в виде:

Заметим также, что в пределе при d → ∞ функция Гаусса 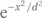становится постоянной и равной единице. Отсюда следует, что

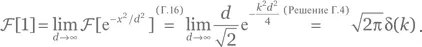
Решение для упражнения Г.8.Для начала установим a = 1. Заметим, что требуемый интеграл представляет собой, с точностью до множителя 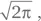преобразование Фурье от функции 𝑓( x ) = 1 в точке — k . Применив (Г.18), находим:

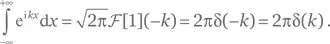
Здесь мы воспользовались четностью дельта-функции, которая очевидна из (Г.1). Чтобы обобщить этот результат для произвольного a , используем (Г.12).

Решение для упражнения Г.9.

a) Применяя результаты (Г.13) и (Г.17), получаем:

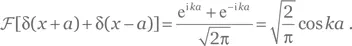
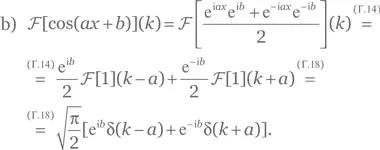
Решение для упражнения Г.10

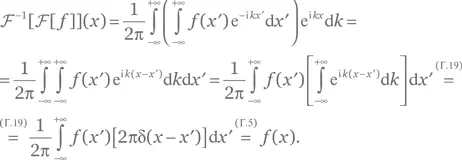
Решение для упражнения Г.11.Начнем с определения (Г.21) обратного преобразования Фурье и получим:

[здесь мы поменяли местами переменные x и k по отношению к (Г.21)]. Второе равенство в (Г.23) получается заменой х на — х в уравнении выше.

АЛЕКСАНДР ЛЬВОВСКИЙ(45) — физик-экспериментатор в области квантовых оптических технологий. Родился и вырос в Москве, учился в 91-й и 57-й школах, окончил Московский физико-технический институт и Колумбийский университет в Нью-Йорке, где получил в 1998 году степень доктора философии. После этого провел год в Калифорнийском университете в Беркли в качестве постдока, а затем пять лет в Университете Констанца в Германии: сначала в качестве стипендиата имени Александра фон Гумбольдта, а затем руководителя группы в рамках гранта имени Эмми Нётер Немецкого научного общества.

В 2004 году стал профессором факультета физики и астрономии в Университете Калгари, а с осени 2018 года является профессором в Оксфордском университете в Великобритании, параллельно с 2013 года руководит лабораторией в Российском квантовом центре.

Александр Львовский — пожизненный член Американского физического общества, почетный член (fellow) Американского оптического общества и лауреат ряда наград, в частности Международной премии по квантовым коммуникациям, гранта Alberta Ingenuity и личной грамоты от премьер-министра Канады. О его работах рассказывали многие СМИ, такие как CBC, Daily Mail, MIT Technology Review , NBC, New Scientist, Wired , ТАСС, Первый канал, телеканалы «Россия» и «Культура».

Переводчик Н. Лисова

Редактор А. Ростоцкая

Руководитель проекта А. Тарасова

Корректоры Е. Аксёнова, М. Миловидова

Компьютерная верстка А. Фоминов

Дизайн обложки Ю. Буга

Иллюстрации на обложке Shutterstock.com

Подробнее об этом лозунге, ошибочно приписываемом Фейнману, см. в разд. 2.4.