Александр Львовский - Отличная квантовая механика

Это, конечно, фигура речи. Фотоны движутся со скоростью света, и никто не может «иметь» их на протяжении сколько-нибудь продолжительного периода времени. Утверждения о том, что у Алисы и Боба «имеется» фотон, относятся, как правило, к моменту времени непосредственно перед измерением.

Три эквивалентные части соотношения (2.1) представляют собой альтернативные варианты записи для состояний, представляющих собой тензорные произведения; мы будем считать эти варианты взаимозаменяемыми и использовать попеременно. Обратите внимание: индекс A (Алиса) или B (Боб), отмечающий принадлежность гильбертова пространства, помещается снаружи от кет-скобки. Если эти индексы опущены, то считается, что первый компонент тензорного произведения всегда относится к Алисе, а второй — к Бобу.

В первый раз эта схема была предложена и реализована в: P. G. Kwiat, E. Waks, A. G. White, I. Appelbaum, and P. H. Eberhard, Ultrabright source of polarization-entangled photons , Physical Review A 60, R773 (R) (1999).

Как правило, мы будем использовать интуитивно понятные двухиндексные обозначения для матриц состояний и операторов в составных гильбертовых пространствах. То есть каждый элемент |𝑣i⟩ ⊗ |ωj⟩ базиса тензорного произведения идентифицируется парой индексов ( i, j ), как в (2.8). Это означает, в частности, что матрица оператора имеет четыре, а не два, индекса.

W. Wootters, W. Zurek, A Single Quantum Cannot be Cloned, Nature 299, 802 (1982); D. Dieks, Communication by EPR devices, Physics Letters A 92, 271 (1982).

Порядок символов внутри бра-вектора такой же, как и внутри кет-вектора: первый символ относится к Алисе, второй — к Бобу. Индексы A и B, указывающие на конкретные гильбертовы пространства, если они есть, обычно помещаются слева от бра-векторов.

Напоминание: кубит есть любое двумерное гильбертово пространство. Примером кубита может служить поляризация фотона.

Возможно, кому-то захочется ответить, что когда фотон Алисы пропадает из состояния, к примеру, 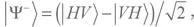то фотон Боба приобретает состояние 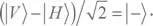Это, разумеется, неверно. Чтобы убедиться в этом, вспомните упр. 2.9, где мы выяснили, что |Ψ —⟩ можно также записать, как (|+ —⟩ — |— +⟩)/2. Это означает, что фотон Боба с равной вероятностью может находиться в состояниях |+⟩ и |—⟩.

Тот факт, что ансамбли Боба, полученные для двух измерительных базисов Алисы, идентичны, мы покажем строго в упр. 5.40.

A. Einstein, B. Podolsky, N. Rosen, Can Quantum-Mechanical Description of Physical Reality be Considered Complete? Physical Review 47, 777 (1935).

D. Bohm, Quantum Theory, Prentice-Hall, Englewood Cliffs, 1951.

Фок В. А., Эйнштейн А., Подольский Б. и др. Можно ли считать, что квантово-механическое описание физической реальности является полным? // Успехи физических наук. Т. XVI. Вып. 4 (1936). С. 440. — Прим. ред.

Там же. С. 446. — Прим. ред.

J. S. Bell, On the Einstein — Poldolsky — Rosen paradox, Physics 1, 195 (1964).

S. J. Freedman and J. F. Clauser, Experimental test of local hidden-variable theories , Physical Review Letters 28, 938 (1972).

A. Aspect, P. Grangier, G. Roger, Experimental Realization of Einstein — Podolsky — Rosen — Bohm Gedankenexperiment: A New Violation of Bell’s Inequalities , Physical Review Letters 49, 91 (1982).

G. Weihs, T. Jennewein, C. Simon, H. Weinfurter, A. Zeilinger, Violation of Bell’s inequality under strict Einstein locality conditions , Physical Review Letters 81, 5039 (1998).

M. A. Rowe, D. Kielpinski, V. Meyer, C. A. Sackett, W. M. Itano, C. Monroe, D. J. Wineland, Experimental violation of a Bell’s inequality with efficient detection , Nature 409, 791 (2001).

B. Hensen et al ., Loophole-free Bell inequality violation using electron spins separated by 1.3 kilometres , Nature 526, 682 (2015).

M. Guistina et al. Significant-loophole-free test of Bell’s theorem with entangled photons , Physical Review Letters 115, 250401 (2015).

L. K. Shalm et al. A strong loophole-free test of local realism , Physical Review Letters 115, 250402 (2015).

Конечно, можно настроить электронику таким образом, что при отсутствии сигнала в обоих детекторах экран случайным образом покажет величину ±1. При такой программе эксперимент будет соответствовать рис. 2.2, но проблему это не решит (см. упр. 2.52).

Теоретическая идея: D. M. Greenberger, M. A. Horne, A. Shimony, A. Zeilinger, in Bell ’ s Theorem, Quantum Theory, and Conceptions of the Universe (M. Kafatos, ed.), p. 73 (Kluwer Academic, Dordrecht, 1989). Эксперимент: J. W. Pan, D. Bouwmeester, M. Daniell, H. Weinfurter and A. Zeilinger, Experimental test of quantum nonlocality in three-photon GHZ entanglement, Nature 403, 515 (2000).

Этот стандартный подход к квантовым измерениям называют копенгагенской интерпретацией в честь Нильса Бора.

Может показаться, что (2.33) эквивалентно квантовому клонированию (подразд. 2.1.3), потому что для каждого элемента базиса системы прибор эволюционирует в соответствующий элемент базиса своего гильбертова пространства. На самом деле это не так. Настоящая операция клонирования клонировала бы также и состояния суперпозиции, т. е. переводила бы правую сторону уравнения (2.33) в вид 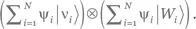Преобразование (2.33) этого не делает и, следовательно, не противоречит теореме о запрете клонирования.

Для удобства будем предполагать, что фотон не уничтожается в ходе обнаружения, и не будем учитывать тот факт, что горизонтальные и вертикальные фотоны следуют по разным пространственным траекториям.

Эта процедура известна как мысленный эксперимент Юджина Вигнера, который поставил себя на позицию Боба, а своего гипотетического друга — на позицию Алисы.

Такой «инструментальный» подход особенно привлекал Ричарда Фейнмана, взгляды которого хорошо отражает выдуманный лозунг «Заткнись и считай» («Shut up and calculate»).

О точном виде собственного состояния импульса речь пойдет в следующей главе; пока же достаточно (2.35).

W. H. Zurek, Decoherence, einselection, and the quantum origins of the classical, Reviews of Modern Physics 75, 715 (2003).

Такие столкновения называются упругими.

E. Schrödinger, Die gegenwartige Situation in der Quantenmechanik , Naturwissenschaften 23, 807–812, 823–828, 844–849 (1935).

Состояние фотона я опустил для краткости.

Этот вывод сделан на основе статей W. H. Zurek, Environment-Assisted Invariance, Entanglement, and Probabilities in Quantum Physics, Physical Review Letters 90, 120404 (2003); Probabilities from entanglement, Born ’ s rule from invariance, Physical Review A 71, 052105 (2005).

Обратите внимание: выходное значение целевого кубита соответствует результату действия вентиля «исключающее ИЛИ» (XOR).