Александр Львовский - Отличная квантовая механика
- Название:Отличная квантовая механика
- Автор:
- Жанр:
- Издательство:Альпина нон-фикшн
- Год:2019
- Город:Москва
- ISBN:978-5-0013-9162-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Александр Львовский - Отличная квантовая механика краткое содержание
В книге применяется математически простая физическая система — поляризация фотонов — в качестве инструмента визуализации, что позволяет студенту увидеть запутанную красоту квантового мира с самых первых страниц. Формальные концепции квантовой физики проиллюстрированы примерами из современных экспериментальных исследований, таких как квантовые компьютеры, коммуникации, телепортация и нелокальность.
Материал книги успешно использовался в качестве основного учебного пособия в двухсеместровом курсе по квантовой механике для студентов-физиков. Однако потенциальный круг читателей много шире и охватывает как студентов и аспирантов, изучающих точные науки, так и всех интересующихся квантовой физикой и квантовыми технологиями. Математический аппарат, требующийся для понимания книги, не выходит за пределы курса технического вуза или математической школы.
Автор — профессор Оксфордского университета, экспериментатор с мировым именем в области квантовой оптики и квантовой информатики — применяет сократовскую педагогику: студенту предлагается самостоятельно разработать аппарат квантовой физики путем последовательного решения тщательно составленных задач. Подробные решения представлены во втором томе пособия.
Отличная квантовая механика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
71
Теоретическая идея о квантовой телепортации впервые была опубликована в C. H. Bennett, G. Brassard, C. Crépeau, R. Jozsa, A. Peres, W. K. Wootters, Teleporting an Unknown Quantum State via Dual Classical and Einstein — Podolsky — Rosen Channels, Physical Review Letters 70, 1895–1899 (1993). Первые эксперименты (устроенные по-разному) были проведены почти одновременно несколькими группами: D. Bouwmeester, J.-W. Pan, K. Mattle, M. Eibl, H. Weinfurter, A. Zeilinger, Experimental Quantum Teleportation, Nature 390, 6660, 575–579 (1997); D. Boschi, S. Branca, F. De Martini, L. Hardy, S. Popescu, Experimental Realization of Teleporting an Unknown Pure Quantum State via Dual classical and Einstein — Podolsky — Rosen channels, Physical Review Letters 80, 1121–1125 (1998); A. Furusawa, J. L. Sorensen, S. L. Braunstein, C. A. Fuchs, H. J. Kimble, E. S. Polzik, Unconditional quantum teleportation, Science 282, 706–709 (1998).
72
Теоретическая идея: M. Żukowski, A. Zeilinger, M. A. Horne, and A. K. Ekert, «Event-ready detectors»: Bell experiment via entanglement swapping, Physical Review Letters 71, 4287 (1993). Эксперимент: J.-W. Pan, D. Bouwmeester, H. Weinfurter, and A. Zeilinger, Experimental Entanglement Swapping: Entangling Photons That Never Interacted, Physical Review Letters 80, 3891 (1998).
73
A. I. Lvovsky, B. C. Sanders, and W. Tittel, Optical Quantum Memory, Nature Photonics 3, 706–714 (2009); N. Sangouard, C. Simon, H. De Riedmatten, and N. Gisin, Quantum repeaters based on atomic ensembles and linear optics, Reviews of Modern Physics 83, 3380 (2011).
74
Если вы не знакомы с дельта-функцией Дирака и преобразованием Фурье, то, прежде чем продолжить, просмотрите, пожалуйста, разделы Г.1 и Г.2 в соответствующем приложении.
75
Почему континуум координатных собственных состояний порождает гильбертово пространство бесконечной размерности, тогда как континуум линейно поляризованных состояний — всего лишь двумерное гильбертово пространство? Если не помните ответа, загляните в разд. 1.3.
76
Для более строгого рассмотрения этого вопроса вводится специальная конструкция, разработанная И. М. Гельфандом и Н. Я. Виленкиным и именуемая оснащенным гильбертовым пространством (rigged Hilbert space). Подробности в: R. de la Madrid, The role of the rigged Hilbert space in quantum mechanics, European Journal of Physics 26, 287 (2005).
77
На самом деле оригинальная формулировка Гейзенберга была немного иной (см. отступление 3.3).
78
Решение можно найти, к примеру, в: Ulf Leonhardt, Measuring the quantum state of light (Cambridge University Press, 1997).
79
W. Heisenberg, Über den anschaulichen Inhalt der quantentheoretischen Kinematik und Mechanik , Zeitschrift für Physik 43, 172 (1927).
80
Гейзенберг В. О наглядном содержании квантовотеоретической кинематики и механики // Успехи физических наук. Т. 122. Вып. 8 (1977). С. 654. — Прим. ред.
81
Пример предоставлен А. В. Белинским и В. Б. Лапшиным.
82
На самом деле фазовая скорость волны де Бройля — вопрос скорее договоренности, чем физики. Предположим, мы сдвигаем точку начала отсчета потенциальной энергии на — V 0, так что частица теперь имеет постоянный потенциал V ( x ) = V 0. То же физическое состояние, что и в (3.56), теперь будет обладать энергией E + V 0, так что его волновая функция приобретет следующую зависимость от времени:
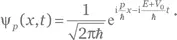
Пространственное поведение этой волновой функции такое же, как в (3.56), потому что оно определяется импульсом, а последний связан с кинетической энергией, которая не изменилась. Но эволюция во времени будет зависеть от V 0, поскольку частота волны теперь равняется ( E + V 0)/ℏ, а не E /ℏ. Таким образом, фазовая скорость тоже будет зависеть от V 0.
Групповая же скорость пропорциональна производной энергии и потому не зависит от выбора точки отсчета потенциала.
83
J. P. Gordon, H. J. Zeiger, and C. H. Townes, Molecular Microwave Oscillator and New Hyperfine Structure in the Microwave Spectrum of NH3 , Physical Review 95, 282 (1954); J. P. Gordon, H. J. Zeiger, and C. H. Townes, The Maser — New Type of Microwave Amplifier, Frequency Standard, and Spectrometer , Physical Review 99, 1264 (1955).
84
Подчеркну разницу между векторами |0⟩ и |zero⟩ (см. определение A.1). Вектор |zero⟩ есть нулевой вектор гильбертова пространства, такой что для любого вектора |ψ⟩ мы имеем |ψ⟩ + |zero⟩ = |ψ⟩. Его норма равна ⟨zero|zero⟩ = 0, поэтому данный вектор не представляет никакого физического квантового состояния. Вакуумное состояние |0⟩, напротив, есть физическое состояние: ⟨0|0⟩ = 1 и |ψ⟩ + |0⟩ ≠ |ψ⟩.
85
Эти утверждения верны в некоторых пределах, поскольку физические модели гармонического осциллятора или двухуровневой системы могут не выдержать слишком сильного возбуждения. Так случается, к примеру, если качели взлетают слишком высоко, они выходят за рамки приближения маятника с ее допущением о малости угла. А электрическое поле в импульсе лазера может быть настолько мощным, что атом ионизуется.
86
На самом деле эта окружность имеет не только символическое значение. Поведение неопределенностей в фазовом пространстве описывается так называемой функцией Вигнера, которая является аналогом классической плотности вероятности в фазовом пространстве.
87
В данном разделе мы считаем, что гамильтониан явно не зависит от времени.
88
Мы ограничиваемся одномерным движением.
89
Тот факт, что гамильтониан, если он не зависит явно от времени, в представлении Гейзенберга не эволюционирует, можно рассматривать как квантовый аналог классического закона сохранения энергии.
90
Обратите внимание, что смещение на положительную величину X 0соответствует отрицательному изменению аргумента волновой функции. Подробнее об этом в подразд. 3.9.3.
91
Преобразование операторов осциллятора, заданное уравнениями (3.173), (3.174) или (3.180), (3.181), называется преобразованием Боголюбова.
92
Во всех последующих задачах используйте перемасштабированные наблюдаемые координаты и импульса, т. е. 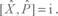
93
Данное состояние иногда называют «кошкой Шрёдингера», хотя оно и не полностью соответствует оригинальному мысленному эксперименту Шрёдингера с запутанностью между микроскопическим и макроскопическим объектом. Тем не менее это суперпозиция двух «классических» и потенциально макроскопических когерентных состояний, поэтому оно в высшей степени неклассично. Построение таких состояний со все бóльшими амплитудами α может помочь нам определить пределы применимости квантовой физики — см. подразд. 2.4.3. Поэтому они являются предметом активного изучения.
94
Чтобы избежать путаницы, мы не будем в этой главе использовать термин «вектор» в смысле «элемент гильбертова пространства». Будем применять его только для обозначения наблюдаемых, имеющих x -, y - и z -компоненты.
95
Иногда мы будем пользоваться альтернативной системой записи, имеющей такой вид: 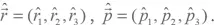
Интервал:
Закладка:








