Александр Львовский - Отличная квантовая механика

Решение для упражнения В.6.Показатели преломления n e и n o изменяют длину обыкновенной волны согласно λo = λ/ n o, а необыкновенной — согласно λe = λ/ n e, что соответствует волновым числам k e = 2π n e/λ и k o = 2π n o/λ. Проходя сквозь кристалл, эти волны приобретают фазы ϕe = k e L и ϕo = k o L , так что Δϕ = 2π( n e — n o) L /λ.

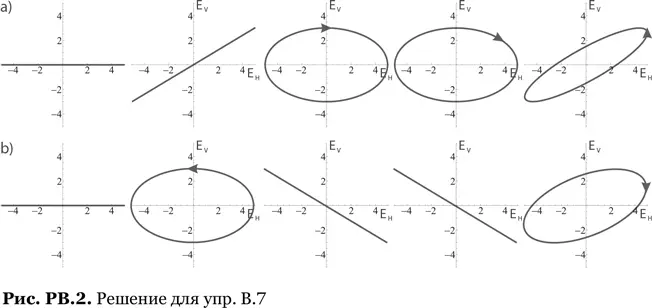
Решение для упражнения В.7.Полуволновые и четвертьволновые пластинки с вертикальными оптическими осями сдвинут фазу вертикального компонента поля на π и π/2 соответственно. См. рис. РВ.2.

Решение для упражнения В.9.Картины линейной поляризации с углами ±45° соответствуют A H = ± A V и ϕH = ϕV + m π, где m — целое число. Сравнивая это условие с условием из упр. В.4(b), находим, что волны с поляризацией ±45° и круговой поляризацией получаются друг из друга путем добавления ±π/2 к ϕV — а это в точности то, что делает четвертьволновая пластинка.

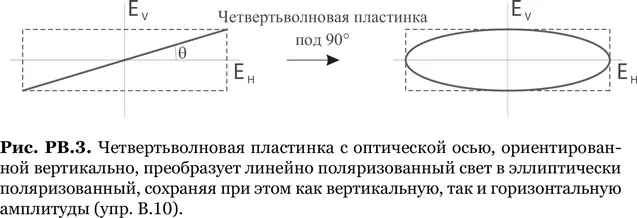
Решение для упражнения В.10.Линейная поляризация под углом θ подразумевает, что A H = A cosθ, A V = A sinθ, где A действительно и положительно, а ϕH — ϕV = 0. Без потери общности мы можем считать, что ϕH = ϕV = 0. Перед волновой пластинкой у нас такая картина:

E H ( z,t ) = A cosθcos( kz — ω t ); (РВ.6)

E V ( z,t ) = A sinθcos( kz — ω t ),

а после нее —

E H ( z,t ) = A cosθcos( kz — ω t ); (РВ.7)

E V ( z,t ) = A sinθcos( kz — ω t + π/2) = — A sinθsin( kz — ω t ).

Из последнего результата следует, что

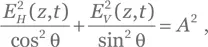
а это уравнение эллипса, оси которого ориентированы вертикально и горизонтально, причем отношение длин осей равно cos θ/sin θ (рис. РВ.3).

Решение для упражнения В.11.Как мы знаем из упр. В.5, в общем случае картина поляризации является эллиптической. Предположим, что амплитуды желаемой поляризационной картины вдоль большой и малой полуосей равны A 1и A 2, а большая ось ориентирована под углом β к горизонтали. Обозначим θ = tg –1( A 2/ A 1) и 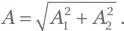Для начала возьмем горизонтально поляризованный свет амплитуды A и применим к нему четвертьволновую пластинку под углом θ к горизонтали. В системе отсчета волновой пластинки это действие эквивалентно применению четвертьволновой пластинки с вертикальной оптической осью к линейной поляризации с углом —θ. Следуя логике предыдущего упражнения, мы получаем эллиптическую картину с осями, расположенными вдоль и поперек оптической оси пластинки и с соотношением длин осей cosθ/sinθ = A 1/ A 2. А в лабораторной системе отсчета этот эллипс расположен под углом θ к горизонту. Остается повернуть данный эллипс, это достигается при помощи полуволновой пластинки под углом (β + θ)/2 (рис. РВ.4).

Решение для упражнения В.12.В системе отсчета, ориентированной под углом 45° по отношению к лабораторной системе отсчета, оптическая ось четвертьволновой пластинки вертикальна. Линейно поляризованный свет, проходящий через эту волновую пластинку, порождает картину, описываемую уравнением

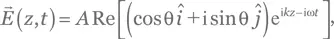
где θ — угол между поляризацией и осью волновой пластинки, а 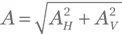(см. упр. В.10). Чтобы перейти к лабораторной системе отсчета, мы поворачиваем вектор поля в плоскости x — y на 45° при помощи матрицы, найденной в упр. A.41,

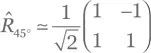
и находим

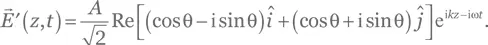
Это соответствует одинаковой интенсивности A 2(cosθ 2+ sin 2θ)/2 = A 2/2 для горизонтальной и вертикальной поляризации.

Такой результат несложно представить себе зрительно, заметив, что преобразование линейной схемы в системе отсчета четвертьволновой пластинки (рис. РВ.3) дает эллиптическую картину, симметричную относительно осей ±45° (они соответствуют горизонтальной и вертикальной осям в лабораторной системе отсчета) и, следовательно, содержащую равное количество энергии в проекциях на эти оси.

Глава РГ

Решение для упражнения Г.1.Воспользовавшись методом интегрирования по частям, находим

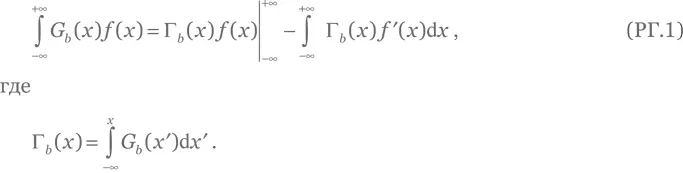
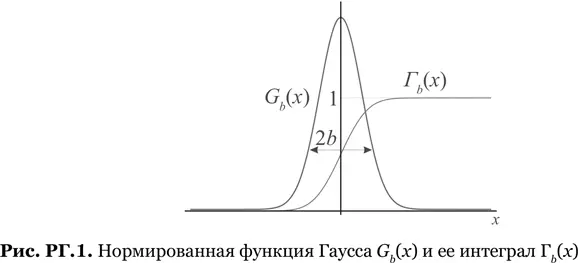
Первый член в правой части уравнения (РГ.1) равен 𝑓(+∞) при ограниченной 𝑓( x ). Чтобы оценить второй член, проанализируем поведение функции Γb( x ) (рис. РГ.1). Она приближается к 0 при —∞, к 1 при +∞ и значительно отличается от этих значений в области, где G b( x ) заметно отличается от нуля. Ширина данной области обнуляется при b → 0. В этом пределе Γb( x ) ведет себя как ступенчатая функция Хевисайда (Г.7). Следовательно, при гладкой 𝑓( x )

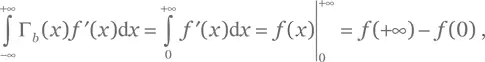
согласно формуле Ньютона — Лейбница. Подставив оба члена в (РГ.1), получаем 𝑓(0).

Решение для упражнения Г.2

a) Уравнение (Г.4) получаем, подставив 𝑓( x ) = 1 в уравнение (Г.3).

b) Произведем замену переменной интегрирования x — a = t . Тогда d t = d x и

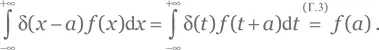
c) Рассмотрим гладкую функцию 𝑓( x ) и интеграл:

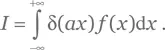
Чтобы вычислить этот интеграл, заменим переменную интегрирования ax = t , так что d x = d t / a . Тогда для положительного a :

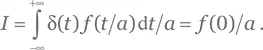
Если a отрицательно, x = ±∞ соответствует t = ∓∞, так что нам придется изменить пределы интегрирования: