Александр Львовский - Отличная квантовая механика

Мы можем также решить эту задачу, использовав результат предыдущего упражнения:

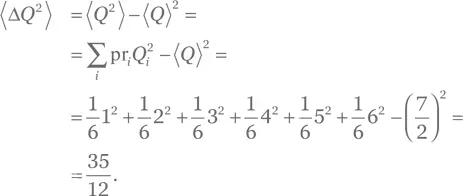
Решение для упражнения Б.4.Величину QR можно рассматривать как случайную переменную, которая принимает значение Q i R j, если Q i и R j имеют место одновременно, что происходит с вероятностью для каждой пары ( i, j ). Теперь, применив определение математического ожидания, находим

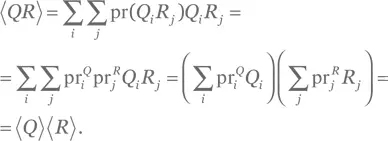
Если Q и R не являются независимыми, то утверждение, что Q i и R j происходят одновременно с вероятностью 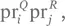неверно, как неверно и равенство ⟨ QR ⟩ = ⟨ Q ⟩⟨ R ⟩. Так, если Q = R , то ⟨ QR ⟩ = ⟨ Q 2⟩ ≠ ⟨ Q ⟩ 2= ⟨ Q ⟩⟨ R ⟩.

Решение для упражнения Б.5.Мы можем рассматривать каждый k -й бросок кости как независимую случайную переменную Q (k ). Тогда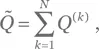

Последнее выражение содержит N 2членов, из которых в N членов k равно ℓ, а в N ( N — 1) членов k не равно ℓ. Для k = ℓ имеет место равенство ⟨ Q (k ) Q (ℓ )⟩ = ⟨ Q 2⟩; в противном случае ⟨ Q (k ) Q (ℓ )⟩ = ⟨ Q ⟩ 2согласно упр. Б.4. Отсюда следует, что

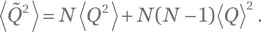
Для дисперсии воспользуемся (Б.3), чтобы записать:

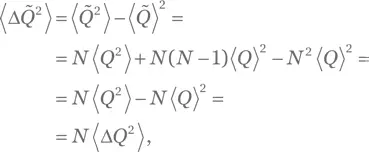
и далее, для среднеквадратического отклонения:

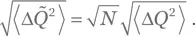
Решение для упражнения Б.6.Воспользовавшись (Б.5), находим 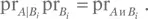Поскольку события B i несовместны, имеет место равенство Последняя величина равна prA, потому что события B i коллективно исчерпывающи, т. е. событие ( B 1или … или B n) происходит наверняка.

Решение для упражнения Б.7

a) Согласно (Б.5), имеет место равенство

pr полож.|неинф.= pr полож.&неинф./pr неинф.,

поэтому

pr полож.&неинф.= pr полож.|неинф.× pr неинф.= pr полож.|неинф.[1-pr инф.] = 0,04995.

b) Разделим всех людей с положительным результатом на два подмножества — инфицированные и неинфицированные:

pr полож.= pr полож.&неинф.+ pr полож.&инф.= pr полож.&неинф.+ pr инф.= 0,051.

Второе равенство в этом выражении верно, поскольку тест не дает ложных отрицательных результатов, т. е. множество людей, которые инфицированы и показывают положительный результат, — это то же множество людей, которые просто инфицированы.

c) Пользуясь двумя предыдущими результатами, находим:

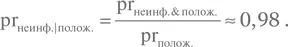
Такой итог может показаться удивительным. Хотя результат Алисы положителен, вероятность того, что она и в самом деле инфицирована, очень низка — потому что еще более низка доля людей, которые инфицированы в действительности. Положительный результат для случайного человека, скорее всего, ошибочен, несмотря на низкий процент ложных положительных результатов, указанный в спецификации теста.

Решение для упражнения Б.8

a) Каждый из n бросков представляет собой независимое случайное событие. Поэтому существует 2n возможных цепочек исходов длины n , и вероятность любой конкретной цепочки равна 1/2n. Среди этих цепочек есть таких, в которых в k подбрасываниях монета выпадает орлом, а в n — k — решкой. Отсюда ответ: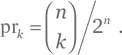

b) В данном случае вероятность любой конкретной последовательности, содержащей k выпадений монеты орлом и n — k — решкой, равна p k (1 — p )n — k. Поэтому ответ из пункта a) становится таким: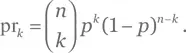

Решение для упражнения Б.10.Для среднего значения имеет место равенство:

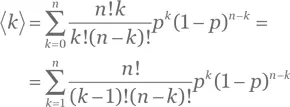
(обратите внимание, мы заменили нижний предел суммирования, потому что слагаемое, соответствующее k = 0, равно нулю). Теперь, заменив переменную суммирования на m = k — 1, находим

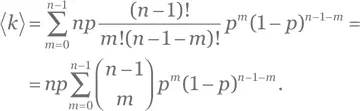
В данном уравнении выражение под знаком суммы — это биномиальная вероятность, соответствующая m успешным исходам из n — 1 событий. Сумма этих вероятностей по всем значениям m равна 1. Поэтому ⟨ k ⟩ = np .

Для среднего квадрата, действуя аналогичным образом, находим

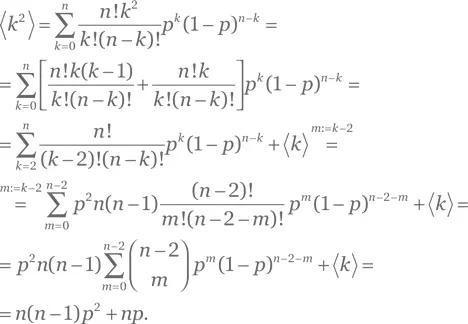
Отсюда следует, что

⟨Δ k 2⟩ = ⟨ k 2⟩ — ⟨ k ⟩ 2= np — np 2.

Решение для упражнения Б.11

a) Вероятность рождения ребенка на единицу населения в день ( p ) равна 10/100 000 = 10 –4. Используя биномиальное распределение с n = 100 000, находим:

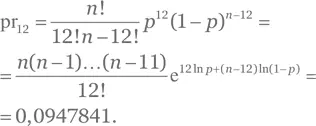
b) Аналогичным образом находим pr 12= 0,0947807.

Решение для упражнения Б.12

Решение для упражнения Б.13

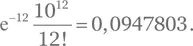
Решение для упражнения Б.15.В пределе при p → 0, n → ∞, λ = pn = const уравнение (Б.8) принимает вид