Александр Львовский - Отличная квантовая механика

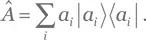
Экспонента этого оператора

имеет те же собственные векторы, но ее собственные значения — 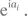Поскольку все a i действительны, все имеют абсолютные значения, равные единице, поэтому e iÂунитарен, согласно упр. A.83.

В то же время 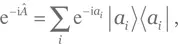так что

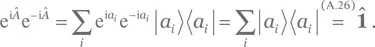
Решение для упражнения A.93.В каноническом базисе оператор 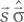характеризуется следующей матрицей:

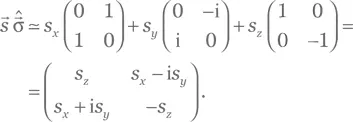
Эта матрица эрмитова, следовательно (согласно упр. A.60), у оператора 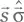два собственных значения 𝑣 1,2и два соответствующих им ортогональных собственных вектора |𝑣 1,2⟩. Собственные значения находятся путем решения характеристического уравнения:

Поскольку 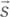— вектор единичной длины, собственные значения равны 𝑣 1,2= ±1 и, таким образом,

Теперь мы можем записать экспоненту оператора как

Хотя мы и не нашли явного выражения для |𝑣 1⟩ и |𝑣 2⟩, мы знаем из (A.50), что Пользуясь этим и уравнением (РА.49), мы можем переписать (РА.50) как

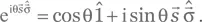
Решение для упражнения A.95.Разложим 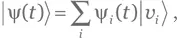где {|𝑣i⟩} — ортонормальный базис, постоянный по отношению к t . Учитывая линейность гильбертова пространства, находим

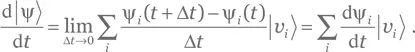
Аналогично, производная оператора с матрицей (Yij( t )) представляет собой матрицу (dYij( t )/d t ).

Решение для упражнения A.96.В ортонормальном базисе {| a i⟩}, который диагонализирует Â , имеет место равенство

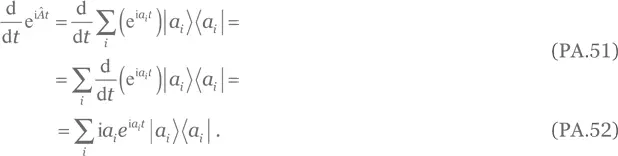
Операторы i  e i Ât и ie i Ât  имеют то же спектральное разложение, что и оператор выше.

Решение для упражнения A.97

a) Воспользуемся разложением Тейлора экспоненциальной функции оператора, чтобы записать

b) Начнем с того, что воспользуемся результатом упр. A.96 и выведем

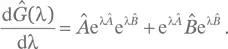
Чтобы привести этот результат к виду правой части уравнения (A.56), нам нужно поставить и Â , и 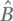справа от экспонент. Каждый из этих операторов коммутирует с экспонентой самого себя (упр. A.90), но, чтобы обменять местами операторы Â и 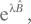необходимо использовать результат пункта a), который мы запишем как Имеем

c) Пусть Взяв производную от обеих частей этого уравнения, получим (A.56):

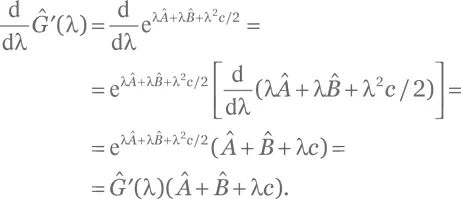
Мы видим, что оба оператора — Ĝ (λ) и Ĝ' (λ) — удовлетворяют уравнению (A.56). Чтобы убедиться в равенстве этих двух операторов, нам нужно также проверить граничное условие Коши, т. е. что Ĝ (λ) = Ĝ' (λ) при λ = 0. И действительно, в этом случае и Ĝ (λ), и Ĝ' (λ) превращаются в оператор тождества, так что равенство выполняется.

d) Для λ = 1 уравнение (A.57) принимает вид

Поскольку c — число, это уравнение эквивалентно формуле Бейкера — Хаусдорфа — Кэмпбелла.

Глава РБ

Решение для упражнения Б.1.Если мы бросим шестигранную игральную кость, то шанс на выпадение ее любой заданной гранью вверх будет равен 1/6. Таким образом, pri = 1/6 для всех i . Величина Q i — значение, обозначенное на выпавшей стороне кости. Подставив эти величины в уравнение для математического ожидания, получаем

Решение для упражнения Б.2.Раскроем выражение в правой части (Б.2) и запишем

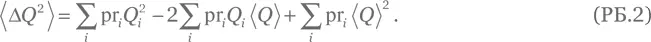
В двух последних слагаемых этого выражения величина ⟨ Q ⟩ одинакова при всех значениях i , поэтому ее можно вынести из-под знака суммы:

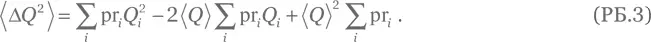
Используя

получаем

⟨Δ Q 2⟩ = ⟨ Q ⟩ − 2⟨ Q ⟩⟨ Q ⟩ + ⟨ Q ⟩ 2= ⟨ Q 2⟩ − ⟨ Q ⟩ 2. (РБ.5)

Решение для упражнения Б.3.Математическое ожидание величины на выпавшей грани кости ⟨ Q ⟩ = 7/2 (см. упр. Б.1), а вероятность каждого из событий равна 1/6. Применив определение неопределенности, вычисляем