Александр Львовский - Отличная квантовая механика
- Название:Отличная квантовая механика
- Автор:
- Жанр:
- Издательство:Альпина нон-фикшн
- Год:2019
- Город:Москва
- ISBN:978-5-0013-9162-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Александр Львовский - Отличная квантовая механика краткое содержание
В книге применяется математически простая физическая система — поляризация фотонов — в качестве инструмента визуализации, что позволяет студенту увидеть запутанную красоту квантового мира с самых первых страниц. Формальные концепции квантовой физики проиллюстрированы примерами из современных экспериментальных исследований, таких как квантовые компьютеры, коммуникации, телепортация и нелокальность.
Материал книги успешно использовался в качестве основного учебного пособия в двухсеместровом курсе по квантовой механике для студентов-физиков. Однако потенциальный круг читателей много шире и охватывает как студентов и аспирантов, изучающих точные науки, так и всех интересующихся квантовой физикой и квантовыми технологиями. Математический аппарат, требующийся для понимания книги, не выходит за пределы курса технического вуза или математической школы.
Автор — профессор Оксфордского университета, экспериментатор с мировым именем в области квантовой оптики и квантовой информатики — применяет сократовскую педагогику: студенту предлагается самостоятельно разработать аппарат квантовой физики путем последовательного решения тщательно составленных задач. Подробные решения представлены во втором томе пособия.
Отличная квантовая механика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
⟨ k ⟩ = np = λ; ⟨Δ k 2⟩ = np — np 2→ λ.
Решение для упражнения Б.16
a) Для заданного дискретизированного распределения вероятность того, что Q попадает в диапазон между Q′ и Q″ , — это сумма вероятностей для всех интервалов, расположенных между этими значениями:
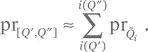
В пределе при δ Q → 0 эта аппроксимация становится равенством, потому что  и
и 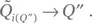 Отсюда, согласно определению (Б.10) непрерывной плотности вероятности, а также определению интеграла, имеет место равенство
Отсюда, согласно определению (Б.10) непрерывной плотности вероятности, а также определению интеграла, имеет место равенство
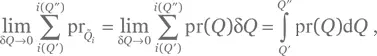
где i ( Q ) — это номер интервала, к которому относится значение Q .
b) Согласно пункту a), интеграл (Б.12) соответствует вероятности обнаружить любое значение Q между —∞ и +∞ и, значит, равен единице.
c) В дискретном случае
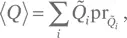
где суммирование проводится по всем интервалам. Переход от суммирования к интегрированию в пределе при δ Q → 0 производится аналогично тому, как это сделано в пункте a).
Решение для упражнения Б.17.Вероятность того, что ядро не распадется через время t от начала эксперимента, равна 2 —t /τ. Тогда вероятность того, что событие распада происходит между моментами t и t + δ t , должна быть пропорциональна производной этой функции, т. е. тоже 2 —t /τс некоторым коэффициентом. Соответственно, pr( t ) = C × 2 —t /τ, где C — постоянная нормирования, которую можно найти при помощи (Б.12):

И это означает, что неопределенность равна
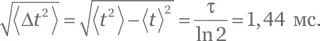
Решение для упражнения Б.18
a) Это следует непосредственно из уравнений (Б.15) и (Б.17).
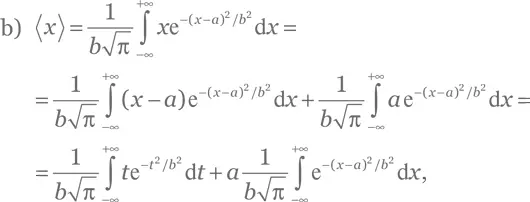
где мы заменили переменную интегрирования в соответствии с t = x — a . Первый член в этом выражении обнуляется, потому что представляет собой интеграл нечетной функции. Второй член равен a , согласно пункту a).

Глава РВ
Решения к упражнениям приложения В
Решение для упражнения В.2.См. рис. РВ.1.

Решение для упражнения В.3.Схема поляризации (В.2) в точке z + Δ z в момент времени t такая же, как в точке z в момент времени t — ( k /ω)Δ z = t — Δ z / c . Поскольку вектор поля есть периодическая функция от времени, сдвиг во времени не изменит форму его траектории.
Решение для упражнения В.4
a) Согласно (В.1),
E H ( z,t ) = A H cos( kz — ω t +ϕ H ); (РВ.1)
E V ( z,t ) = A V cos( kz — ω t +ϕ V ).
Поляризация линейна тогда и только тогда, когда E H ( z,t ) = 0, или E V ( z,t ) = 0, или E H ( z,t ) = λ E V ( z,t ) с некоторым коэффициентом λ. Первые два условия выполняются в том и только том случае, если A H = 0 или A V = 0 соответственно. Третье условие подразумевает, что два косинуса пропорциональны друг другу, а это может произойти тогда и только тогда, когда сдвиг по фазе между ними составляет m π.
b) Для начала обратим внимание: в круговой картине максимальное абсолютное значение для горизонтального и вертикального компонентов должно быть одинаковым, поэтому A H = ± A V. Далее, круговая картина означает, что 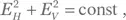 а это подразумевает, что
а это подразумевает, что
cos 2( kz − ω t + ϕ H ) + cos 2( kz − ω t + ϕ V ) = const.
Поскольку cos 2ϕ = (cos 2ϕ+1)/2 для любого ϕ, это условие эквивалентно
cos[2( kz − ω t + ϕ H )] + cos[2( kz − ω t + ϕ V )] = const.
Воспользовавшись еще одним тригонометрическим тождеством: cosϕ + cosθ = 2cos[(ϕ + θ)/2]cos[(ϕ − θ)/2], получим
cos[2( kz − ω t ) + ϕ H + ϕ V ]cos(ϕ H − ϕ V ) = const.
Поскольку первый множитель в левой части приведенного выше условия не может быть константой, это условие выполняется тогда и только тогда, когда cos (ϕH — ϕV) = 0, т. е. 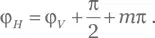
Решение для упражнения В.5.Мы попробуем доказать, что существует множество чисел { A, B, C, D }, не зависящих от z и t , таких, что

где E H( z, t ) и E V( z, t ) — соответственно горизонтальная и вертикальная компоненты волны, задаваемой уравнением (В.1). Из аналитической геометрии известно, что (РВ.2) представляет собой одно из конических сечений: гиперболу, параболу или эллипс. Поскольку и E H, и E V — ограниченные функции, (РВ.2) может описывать только эллипс, крайними случаями которого являются круговая и линейная траектории.
При помощи тригонометрических тождеств запишем (В.1) следующим образом:
E H = A H( c H c — s H s );
E V = A V( c V c — s V s ), (РВ.3),
где мы определили c = cos( kz — ω t ), s = sin( kz — ω t ), c H,V = cos ϕV,H и s H,V = sin ϕV,H. Теперь преобразуем левую часть уравнения (РВ.2):
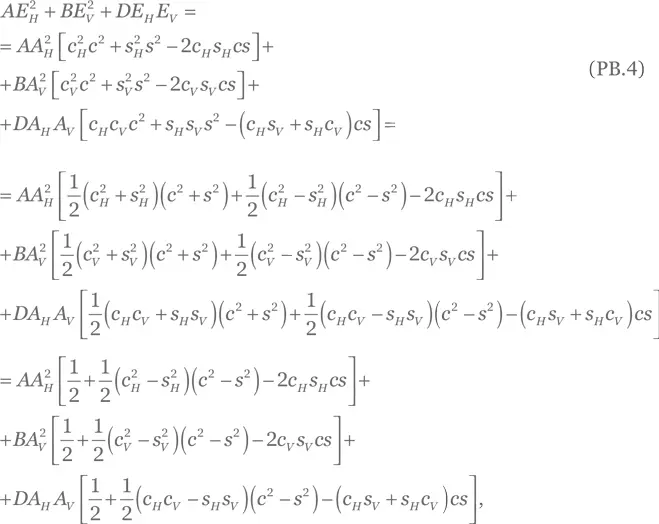
где мы использовали 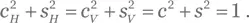 Приведенный результат упрощается до вида
Приведенный результат упрощается до вида
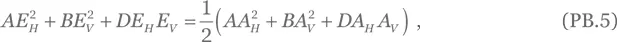
если A, B и D таковы, что коэффициенты перед переменными c 2— s 2и cs , зависящими от ( z, t ), в уравнении (РВ.4) превращаются в нуль:
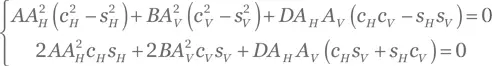
Это система двух уравнений с тремя неизвестными, поэтому она всегда имеет нетривиальное решение. Для данного решения выполняется уравнение (РВ.5), которое идентично уравнению (РВ.2) при 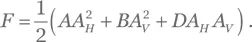
Интервал:
Закладка:








