Александр Львовский - Отличная квантовая механика

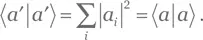
Видим, что оператор Û сохраняет норму | a ⟩ и, следовательно, унитарен.

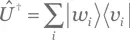Решение для упражнения A.82.Если оператор Û унитарен, то некоторый ортонормальный базис {|ωi⟩} он отображает на другой ортонормальный базис {|𝑣i⟩} (упр. A.81). Отсюда следует, что он может быть записан в виде (упр. A.25). Тогда (упр. A.35). Соответственно,

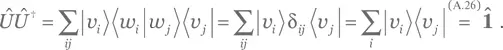
То, что доказывается аналогично.

Теперь докажем, что любой оператор Û , удовлетворяющий 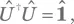сохраняет скалярное произведение двух произвольных векторов | a ⟩ и | b ⟩. Определив | a' ⟩ = Û | a ⟩ и | b' ⟩ = Û | b ⟩, получаем

⟨ a' | b' ⟩ = ⟨ a | Û † Û | b ⟩ = ⟨ a | b ⟩.

Решение для упражнения A.83

a) Так как каждый унитарный оператор Û удовлетворяет 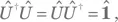утверждение из упр. A.63 выполняется, поэтому Û можно привести к диагональному виду. Для любого собственного значения u и соответствующего ему собственного вектора | u ⟩ имеет место равенство | u' ⟩ = Û | u ⟩ = u | u ⟩, а отсюда вытекает, что

⟨ u' | u' ⟩ = u * u ⟨ u | u ⟩.

Поскольку унитарный оператор сохраняет норму, должно выполняться u * u = | u | 2= 1. Этому удовлетворяет любое u = e iθпри θ ∈ ℝ.

b) Если оператор Û диагонализируем, его матрица в его собственном базисе имеет вид

где u i — собственные значения с абсолютным значением 1 (т. е. такие, что u i * u i = 1). Тогда сопряженная матрица такова:

а произведение этих матриц равно

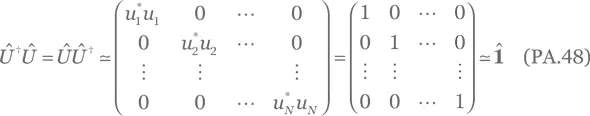
Это показывает, что оператор Û унитарен.

Решение для упражнения A.84

a) Для операторов Паули:

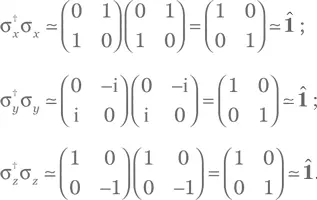
Так что все три оператора Паули унитарны.

b) Для оператора поворота:

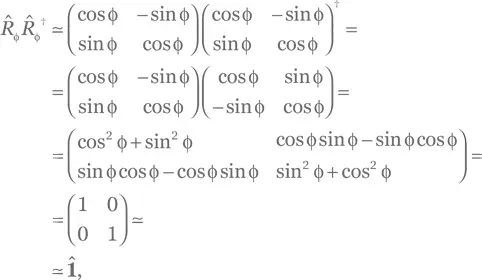
так что этот оператор тоже унитарен. Это можно понять интуитивно: при повороте векторов их длина (норма) не меняется.

Решение для упражнения A.85.Оператор 𝑓( Â ), действующий на вектор | a ⟩, дает

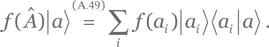
Поскольку Â эрмитов, его собственные векторы ортонормальны. Отсюда все ⟨ a i| a ⟩ = 0, за исключением ситуации, когда | a i⟩ = | a ⟩; в этом случае скалярное произведение равно единице. Следовательно,

𝑓( Â )| a ⟩ = 𝑓( a )| a ⟩⟨ a | a ⟩ = ( a )| a ⟩.

Решение для упражнения A.86.Матрица операторной функции (A.49) в его собственном базисе диагональна с действительными значениями, т. е. является самосопряженной.

Решение для упражнения A.87.Для неотрицательной функции 𝑓( x ) все собственные значения 𝑓( a i) функции оператора (A.49) неотрицательны; это означает, что оператор также неотрицателен, согласно упр. A.72.

Решение для упражнения A.88.Начнем с приведения Â к диагональному виду. Характеристическое уравнение для этой матрицы:

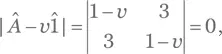
откуда находим собственные значения 𝑣 1,2= {4, –2}. Нормированный собственный вектор, связанный с первым собственным значением, таков:

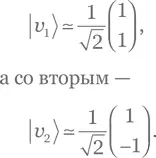
Это означает, что наш оператор можно записать как

 = 4 |𝑣 1⟩⟨𝑣 1|–2 |𝑣 2⟩⟨𝑣 2|.

Теперь применим (A.49) и выразим как

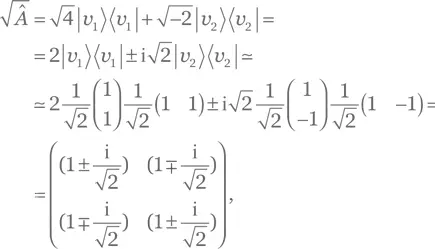
где все матрицы построены в том же базисе, что и матрица Â .

Чтобы определить ln  , нам нужно найти логарифм его собственных значений, одно из которых — 𝑣 2— отрицательно. Логарифм отрицательных чисел не определен в пространстве действительных. В пространстве же комплексных чисел мы можем воспользоваться тем, что e (2 m +1)iπ(где m — произвольное целое число) и, таким образом, e (2 m +1)iπ+ln2= (–1)×2 = –2. Отсюда следует, что ln(–2) = (2 m + 1)iπ + ln2 [151] Логарифм и квадратный корень — примеры многозначных функций, весьма распространенных в комплексном анализе. . В итоге:

Решение для упражнения A.89.Собственные значения Â — это a 1= 0 и a 2= 1 с соответствующими собственными векторами и 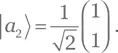Поэтому

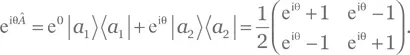
Решение для упражнения A.90.Матрицы Â и 𝑓( Â ) в собственном базисе Â таковы:

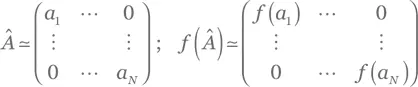
(где a i — собственные значения), и поэтому

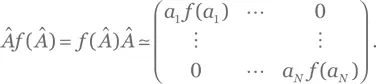
Отсюда [ Â ,𝑓( Â )] = Â 𝑓( Â ) — 𝑓( Â ) Â = 0.

Решение для упражнения A.91

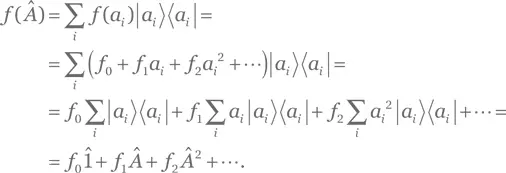
Решение для упражнения A.92.Любой эрмитов оператор может быть приведен к диагональному виду с действительными собственными значениями a i (см. упр. A.60):