Александр Львовский - Отличная квантовая механика
- Название:Отличная квантовая механика
- Автор:
- Жанр:
- Издательство:Альпина нон-фикшн
- Год:2019
- Город:Москва
- ISBN:978-5-0013-9162-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Александр Львовский - Отличная квантовая механика краткое содержание
В книге применяется математически простая физическая система — поляризация фотонов — в качестве инструмента визуализации, что позволяет студенту увидеть запутанную красоту квантового мира с самых первых страниц. Формальные концепции квантовой физики проиллюстрированы примерами из современных экспериментальных исследований, таких как квантовые компьютеры, коммуникации, телепортация и нелокальность.
Материал книги успешно использовался в качестве основного учебного пособия в двухсеместровом курсе по квантовой механике для студентов-физиков. Однако потенциальный круг читателей много шире и охватывает как студентов и аспирантов, изучающих точные науки, так и всех интересующихся квантовой физикой и квантовыми технологиями. Математический аппарат, требующийся для понимания книги, не выходит за пределы курса технического вуза или математической школы.
Автор — профессор Оксфордского университета, экспериментатор с мировым именем в области квантовой оптики и квантовой информатики — применяет сократовскую педагогику: студенту предлагается самостоятельно разработать аппарат квантовой физики путем последовательного решения тщательно составленных задач. Подробные решения представлены во втором томе пособия.
Отличная квантовая механика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
2
Во втором томе русского издания. — Прим. ред.
3
Общепринятых постулатов квантовой механики не существует. Если вы скажете «Это следует из второго закона Ньютона», вас поймут, но утверждения «Это следует из первого постулата квантовой механики» никто не поймет. Вместо этого следует сказать, к примеру, «Это следует из линейности квантового гильбертова пространства».
4
Как в геометрии, которая представляет собой чрезвычайно строгую науку, несмотря на то что первичные понятия в ней, такие как точка, прямая и плоскость, не определены.
5
Это состояние иногда называют кошкой Шрёдингера в честь одного из отцов-основателей квантовой физики Эрвина Шрёдингера. На самом деле Шрёдингер говорил о более сложном объекте, см. отступление 2.5.
6
Если вы не знакомы с понятием поляризации электромагнитной волны, то теперь самое время прочесть первые два раздела приложения В.
7
Может показаться удивительным, что уравнение (1.2) не несет никакой информации о координате фотона по оси z . Причина в том, что этот фотон, будучи квантовой частицей, размазан в пространстве и времени. К факторам, влияющим на степень размазанности, относятся, в частности, характеристики источника, а также «объем квантования», выбранный для теоретического анализа. В случае лазерного луча длина фотона ограничивается длиной когерентности лазера, которая может составлять не один километр. В данной книге мы, как правило, будем считать, что фотоны размазаны на расстояние, намного превышающее размер любого прибора, и потому могут рассматриваться как бесконечно большие.
8
M. Planck, Über das Gesetz der Energieverteilung im Normalspectrum , Annalen der Physik 4, 553 (1901).
9
A. Einstein, Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt , Annalen der Physik 17, 132 (1905).
10
Это явление выражается, в частности, в эффекте давления света, который экспериментально наблюдал Петр Лебедев в 1900 г.
11
Выражение для импульса фотона можно получить также следующим образом. Воспользовавшись знаменитым уравнением Эйнштейна E = mc 2и формулой Планка, мы можем рассчитать массу фотона M = ℏω/ c 2. Фотон движется со скоростью света, следовательно, его импульс равен p = Mc = ℏω/ c .
12
A. H. Compton, A Quantum Theory of the Scattering of X-Rays by Light Elements , Physical Review 21483 (1923).
13
G. N. Lewis, The conservation of photons , Nature 118, 874 (1926).
14
Обсуждение договоренностей, принятых для состояний с круговой (циркулярной), поляризацией, см. в сноске 141.
15
«Мысленный эксперимент» (нем.).
16
Сейчас подходящий момент, чтобы прочитать в приложении разд. В.3.
17
Такие смешанные состояния не являются элементами квантового гильбертова пространства. Подробнее об этом см. подразд. 2.2.4.
18
Хотя мы не знаем, каково это состояние, мы можем многократно приготавливать фотон в одном и том же состоянии путем сохранения постоянных условий эксперимента.
19
Конкретнее, интерферометр Маха — Цендера.
20
Считаем, что линия задержки много короче, чем длина светового импульса, так что изменение задержки не влияет на видность интерференции.
21
Позже мы увидим, что на самом деле фотон может расщепиться на два фотона с меньшей энергией при нелинейном оптическом явлении, известном как параметрическое рассеяние. Однако этот довольно экзотический эффект возникает с низкой вероятностью и только в особых условиях. Наш интерферометр не содержит нелинейных оптических элементов, так что параметрическое рассеяние здесь ни при чем.
22
Именно поэтому, вероятно, популярные книги по квантовой механике любят описывать состояния суперпозиции как состояния, в которых «объект находится в двух разных местах в одно и то же время».
23
«Который путь» (нем.).
24
A. C. Elitzur, L. Vaidman, Quantum mechanical interaction-free measurements , Foundations of Physics 23, 987 (1993).
25
C. H. Bennett, G. Brassard, «Quantum Cryptography: Public Key Distribution and Coin Tossing», Int. Conf. on Computers, Systems and Signal Processing, Bangalore, India (IEEE, New York, 1984), p. 175.
26
P. W. Shor and J. Preskill, Simple Proof of Security of the BB84 Quantum Key Distribution Protocol, Physical Review Letters 85, 441 (2000).
27
На самом деле частота темновых срабатываний может быть выше. Но, поскольку Боб знает точные моменты передачи фотонов Алисой, на частоту ошибки будут влиять только те темновые события, которые произойдут синхронно с щелчками, ожидаемыми от фотонов Алисы.
28
Более полное введение в линейные операторы и матрицы можно найти в разд. A.5 и A.6.
29
Значение индексов x, y и z прояснится в главе 4, когда мы будем изучать квантование момента импульса.
30
Важное исключение здесь — случай, когда матрица имеет вырожденные собственные величины. В этом случае решение для собственного базиса не единственно. Пример см. в упр. A.68.
31
Чтобы узнать о коммутаторах, загляните в разд. A.9.
32
Это не означает, однако, что любое собственное состояние наблюдаемого Â даст определенный результат при измерении 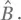 Если у Â есть вырожденные собственные величины, его собственный базис не является единственным (см. разд. A.8), так что не каждый собственный вектор оператора Â гарантированно является также собственным вектором
Если у Â есть вырожденные собственные величины, его собственный базис не является единственным (см. разд. A.8), так что не каждый собственный вектор оператора Â гарантированно является также собственным вектором 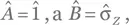 состояние |+⟩ является собственным состоянием Â , но не
состояние |+⟩ является собственным состоянием Â , но не 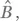 так что наблюдаемое
так что наблюдаемое 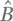 при измерении в этом состоянии будет проявлять неопределенность, несмотря на то что
при измерении в этом состоянии будет проявлять неопределенность, несмотря на то что 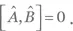
33
Даже если 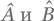 не коммутируют, это не означает, что измерение наблюдаемого
не коммутируют, это не означает, что измерение наблюдаемого 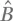 в собственном состоянии наблюдаемого Â всегда дает случайный результат.
в собственном состоянии наблюдаемого Â всегда дает случайный результат.
34
О функциях операторов см. разд. A.11.
35
В данном случае общая фаза в правой части уравнения (1.35) имеет значение. Дело в том, что нас интересует не только преобразование самого состояния |+⟩, но и вся линейная операция, определенная этим преобразованием. Чтобы увидеть действие этой общей фазы, вы можете попытаться решить часть a), заменив (1.35) на |+⟩ → |+⟩.
Читать дальшеИнтервал:
Закладка:








