Александр Львовский - Отличная квантовая механика
- Название:Отличная квантовая механика
- Автор:
- Жанр:
- Издательство:Альпина нон-фикшн
- Год:2019
- Город:Москва
- ISBN:978-5-0013-9162-3
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Александр Львовский - Отличная квантовая механика краткое содержание
В книге применяется математически простая физическая система — поляризация фотонов — в качестве инструмента визуализации, что позволяет студенту увидеть запутанную красоту квантового мира с самых первых страниц. Формальные концепции квантовой физики проиллюстрированы примерами из современных экспериментальных исследований, таких как квантовые компьютеры, коммуникации, телепортация и нелокальность.
Материал книги успешно использовался в качестве основного учебного пособия в двухсеместровом курсе по квантовой механике для студентов-физиков. Однако потенциальный круг читателей много шире и охватывает как студентов и аспирантов, изучающих точные науки, так и всех интересующихся квантовой физикой и квантовыми технологиями. Математический аппарат, требующийся для понимания книги, не выходит за пределы курса технического вуза или математической школы.
Автор — профессор Оксфордского университета, экспериментатор с мировым именем в области квантовой оптики и квантовой информатики — применяет сократовскую педагогику: студенту предлагается самостоятельно разработать аппарат квантовой физики путем последовательного решения тщательно составленных задач. Подробные решения представлены во втором томе пособия.
Отличная квантовая механика - читать онлайн бесплатно ознакомительный отрывок
Интервал:
Закладка:
96
Символ Леви-Чивиты, известный также как антисимметричный единичный тензор третьего ранга, определяется следующим образом:
Для любых j, k, l значение εjkl меняет знак, как только любые два индекса меняются местами. Следовательно, всякий раз, когда любые два индекса равны, εjkl = 0.
ε 123≡ εxyz = 1.
В явном виде:
ε xyz = 1,ε xzy = −1,ε zxy = 1,ε zyx = −1,ε yzx = 1,ε yxz = −1, (4.18)
все остальные εjkl = 0.
97
Как говорилось в разд. 3.3.1 (см. также разд. A.2), символ «≃» означает, что уравнение (4.20) применимо к волновым функциям исключительно в координатном базисе. В полном виде уравнение (4.20) выглядело бы так:
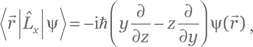
и т. д.
98
Это независимо от того факта, что собственные состояния  вырождены даже в 𝕐, как мы увидим в следующем разделе.
вырождены даже в 𝕐, как мы увидим в следующем разделе.
99
Этот подход — частный случай метода разделения переменных для решения дифференциальных уравнений в частных производных.
100
С тем же успехом мы могли бы выбрать 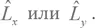 Несколько примеров такого рода мы увидим позже в этом разделе.
Несколько примеров такого рода мы увидим позже в этом разделе.
101
Обозначение |λμ⟩ может ошибочно навести на мысль, что данное состояние представляет собой тензорное произведение. Конечно, это не так: |λμ⟩ есть элемент единственного гильбертова пространства 𝕐.
102
Иногда орбитальное квантовое число l называют просто «момент импульса». Этот термин используется в профессиональном жаргоне, чтобы подчеркнуть, что значение ℏ l есть квантовый эквивалент классического абсолютного значения вектора момента импульса.
103
Стандартное определение сферических гармоник использует связанные полиномы Лежандра. Однако в нашем определении, позаимствованном из книги R. Shankar. Principles of quantum mechanics (Kluwer, 1990), эти полиномы не задействованы, поэтому оно менее громоздко. Этот вид определения соответствует договоренности, которая чаще всего используется в квантовой механике.
104
Множитель (–1)l в уравнение (4.40) добавляется по соглашению.
105
В применении к спину вместо l обычно используется символ s. Символ l зарезервирован для обозначения орбитального момента импульса.
106
Энергии отрицательны, как и ожидалось для связанных состояний.
107
E. Rutherford, The Scattering of α and β Particles by Matter and the Structure of the Atom , Philosophical Magazine 21, 669 (1911).
108
N. Bohr, On the Constitution of Atoms and Molecules , Philosophical Magazine 26, 1–24 and 476–502 (1913).
109
Первоначальная формулировка Менделеева гласила, что периодическая зависимость наблюдается от атомного веса элемента, поскольку в то время атомное ядро еще не было открыто.
110
Магнитное же квантовое число m не влияет на энергию даже в многоэлектронных атомах.
111
Мы используем символ 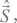 а не
а не 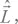 чтобы подчеркнуть, что подпространство l = 2 может соответствовать только спиновой степени свободы.
чтобы подчеркнуть, что подпространство l = 2 может соответствовать только спиновой степени свободы.
112
Изоморфизм 𝑓(⋅) между линейными пространствами 𝕍 и 𝕎 есть взаимно однозначное отображение | a ⟩ ∈ 𝕍 ↦ 𝑓(| a ⟩) ∈ 𝕎, такое что для любых | a ⟩, | b ⟩ ∈ 𝕍 и числа λ
𝑓(| a ⟩ + | b ⟩) = 𝑓(| a ⟩) + 𝑓(| b ⟩); (4.63)
𝑓(λ| a ⟩) = λ𝑓(| a ⟩).
Обратите внимание на разницу между изоморфизмом и линейным оператором (определение A.15). Линейный оператор есть отображение в пределах единого линейного пространства, тогда как изоморфизм может связывать два разных линейных пространства. Кроме того, линейный оператор не обязан быть взаимно однозначным отображением.
113
Определение гиромагнитного отношения см. в Отступлении 4.4.
114
W. Gerlach and O. Stern, Der experimentelle Nachweis der Richtungsquantelung im Magnetfeld, Zeitschrift für Physik 9, 349–352 (1922); W. Gerlach and O. Stern, Das magnetische Moment des Silberatoms, Zeitschrift für Physik 9, 353–355 (1922); W. Gerlach and O. Stern, Der experimentelle Nachweis des magnetischen Moments des Silberatoms, Zeitschrift für Physik 8, 110–111 (1922).
115
В этом разделе мы будем использовать для обозначения частоты Лармора символ Ω 0, а не Ω L.
116
Это магнитное поле обычно называют радиочастотным (rf, radio-frequency), потому что ω, как правило, лежит в диапазоне, где осуществляются радио- и телетрансляции. Поле B 0называют постоянным (dc, direct current) полем.
117
Блоховский вектор в новом базисе получается подстановкой 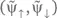 в (4.62) вместо
в (4.62) вместо 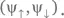
118
В действительности уравнение (4.85) корректно представляет гамильтониан системы в так называемом представлении взаимодействий , которое мы здесь не изучаем.
119
Населенность квантового состояния есть полное число частиц в этом состоянии. В нашем случае населенности состояний со спинами, ориентированными вверх и вниз, равны, соответственно, n pr ↑и n pr ↓, где n — полное число электронов в образце.
120
Обсуждение близкой темы см. в подразд. 3.8.2.
121
Отсылка к тому, что интеграл представляет собой «площадь под кривой».
122
Импульс площадью π соответствует логической операции НЕ над спиновым кубитом: он преобразует |0⟩ = |↑⟩ в |1⟩ = |↓⟩, и наоборот.
123
Математическое представление, связанное с оператором плотности, предложили независимо друг от друга Джон фон Нейман и Лев Ландау в 1927 г. Термины «матрица плотности» и «оператор плотности» традиционно взаимозаменяемы.
124
Обратите внимание, что существование спектрального разложения (5.4) не следует тривиальным образом из определения матрицы плотности (5.1). Два данных выражения очень похожи, но элементы суммы в (5.4) составляют ортонормальный базис, тогда как в (5.1) это просто произвольные состояния.
125
Это верно в случае и стационарного, и вращающегося базиса, поскольку оба они состоят из собственных состояний 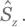
126
Как говорилось в разд. 3.8, квантовое описание моды электромагнитного поля эквивалентно описанию гармонического осциллятора.
127
К примеру, см.: Холево А. С. Вероятностные и статистические аспекты квантовой теории. — М.: Наука, 1980.
128
См. описание эксперимента в: A. G. White, D. F. V. James, W. J. Munro, and P. G. Kwiat, Exploring Hilbert space: Accurate characterization of quantum information, Physical Review A 65, 012301 (2001).
Читать дальшеИнтервал:
Закладка:








