Ричард Фейнман - Том 1. Механика, излучение и теплота

Точки на фиг. 22.1 соответствуют числам, приведенным в табл. 22.4, а соединяющие их линии помогают следить за изменением х и у . Видно, что числа х и у осциллируют; 10 is повторяет себя . Легко объяснить, почему так происходит.

Таблица 22.4. ПОСЛЕДОВАТЕЛЬНЫЕ ПРОИЗВЕДЕНИЯ ЧИСЛА 10 i/8

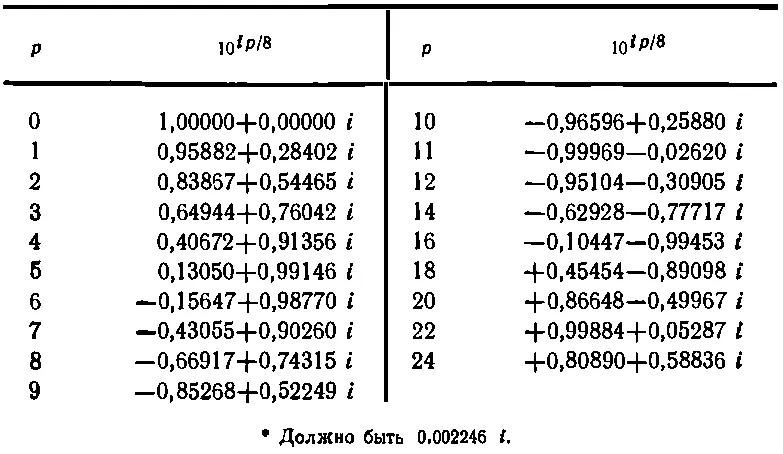
Ведь i в четвертой степени — это i 2 в квадрате . Это число равно единице; следовательно, если 10 0,68iравно i, то, возведя это число в четвертую степень, т. е. вычислив 10 2,72i, мы получим +1. Если нужно получить, например, 10 3,00i, то нужно умножить 10 2,72iна 10 0,28i. Иначе говоря, функция 10 isповторяется, имеет период. Мы уже знаем, как выглядят такие кривые! Они похожи на график синуса или косинуса, и мы назовем их на время алгебраическим синусом и алгебраическим косинусом. Теперь перейдем от основания 10 к натуральному основанию. Это только изменит масштаб горизонтальной оси; мы обозначим 2,3025s через t и напишем 10 is = e it , где t — действительное число. Известно, что e it = x + iy , и мы запишем это число в виде

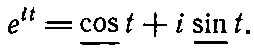(22.8)

Каковы свойства алгебраического косинуса cost и алгебраического синуса sin t ? Прежде всего x 2+ y 2=1; это мы уже доказали, и это верно для любого основания, будь то 10 или е . Следовательно, cos 2t+sin 2t=1. Мы знаем, что e it =1+ it для малых t ; значит, если t — близкое к нулю число, то _cos t близок к единице, a _sin t близок к t . Продолжая дальше, мы придем к выводу, что все свойства этих замечательных функций , получающихся в результате возведения в мнимую степень, в точности совпадают со свойствами тригонометрического синуса и тригонометрического косинуса .

А как обстоит дело с периодом? Давайте найдем его. В какую степень надо возвести е , чтобы получить i? Иными словами, чему равен логарифм i по основанию е? Мы вычислили уже логарифм i по основанию 10; он равен 0,68226i; чтобы перейти к основанию е , мы умножим это число на 2,3025 и получим 1,5709i. Новое число (без i ) можно назвать «алгебраическим π/2». Но поглядите-ка, оно отличается от настоящего π/2 всего лишь последним десятичным знаком, и это просто-напросто следствие наших приближений при вычислениях! Таким образом, чисто алгебраически возникли две новые функции — синус и косинус; они принадлежат алгебре и только алгебре. Мы пошли по их следам и обнаружили, что это те же самые функции, которые так естественно возникают в геометрии. Мы отыскали мост между алгеброй и геометрией.

Подводя итог нашим поискам, мы напишем одну из самых замечательных формул математики

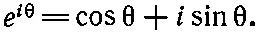(22.9)

Вот она, наша жемчужина.

Связь между алгеброй и геометрией можно использовать для изображения комплексных чисел на плоскости; точка на плоскости определяется координатами х и у (фиг. 22.2).

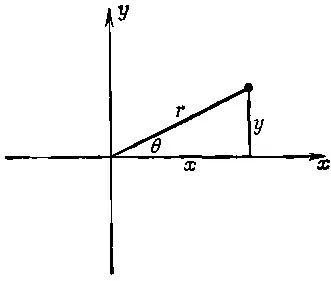
Фиг. 22.2. Комплексное число как точка на плоскости.

Представим каждое комплексное число в виде x+ iy . Если расстояние точки от начала координат обозначить через r, а угол радиуса-вектора точки с осью x — через θ, то выражение x + iy можно представить в виде re i θ. Это следует из геометрических соотношений между x, y, r и θ. Таким образом, мы объединили алгебру и геометрию. Начиная эту главу, мы знали только целые числа и умели их считать. Зато у нас была небольшая идея о могуществе шага в сторону и обобщения. Используя алгебраические «законы», или свойства чисел, сведенные в уравнения (22.1), и определения обратных операций (22.2), мы смогли создать не только новые числа, но и такие полезные вещи, как таблицы логарифмов, степеней и тригонометрические функции (они возникли при возведении действительных чисел в мнимые степени), и все это удалось сделать, извлекая много раз квадратный корень из десяти!

Мы снова будем говорить в этой главе о гармоническом осцилляторе, особенно об осцилляторе, на который действует внешняя сила. Для анализа этих задач нужно развить новую технику. В предыдущей главе мы ввели понятие комплексного числа, которое состоит из действительной и мнимой частей и которое можно изобразить на графике. Действительная часть числа будет изображаться абсциссой, а мнимая — ординатой. Комплексное число а можно записать в виде a = a r + ia i ; при такой записи индекс r отмечает действительную часть а, а индекс i — мнимую. Взглянув на фиг. 23.1, легко сообразить, что комплексное число a = x + iy можно записать и так: x + iy = rexp ( i θ), где r 2= x 2+ y 2=( x + iy )( x - iy )= aa *(а *— это комплексно сопряженное к а число; оно получается из а изменением знака i ).

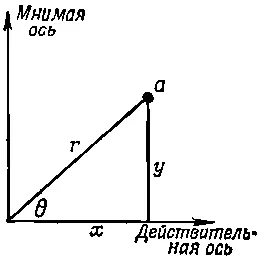
Фиг. 23.1. Комплексное число, изображенное точкой на «комплексной плоскости».

Итак, комплексное число можно представить двумя способами: явно выделить его действительную и мнимую части или задать его модулем r и фазовым углом θ. Если заданы r и θ, то х и у равны rcosθ и rsinθ, и, наоборот, исходя из числа x + iy , можно найти r =√( x 2+ y 2)и угол θ; tgθ равен у / х (т. е. отношению мнимой и действительной частей).

Чтобы применить комплексные числа к решению физических задач, проделаем такой трюк. Когда мы изучали осциллятор, то имели дело с внешней силой, пропорциональной cosωt. Такую силу F = F 0 cos ω t можно рассматривать как действительную часть комплексного числа F =F 0exp(iωt), потому что exp(iωt)=cosωt+isinωt. Такой переход удобен: ведь иметь дело с экспонентой легче, чем с косинусом. Итак, трюк состоит в том, что все относящиеся к осциллятору функции рассматриваются как действительные части каких-то комплексных функций. Найденное нами комплексное число F , разумеется, не настоящая сила, ибо физика не знает комплексных сил: все силы имеют только действительную часть, а мнимой части взяться просто неоткуда. Тем не менее мы будем говорить «сила» F 0 exp ( i ω t ), хотя надо помнить, что речь идет лишь о действительной ее части .