Ричард Фейнман - Том 1. Механика, излучение и теплота

Рассмотрим еще один пример. Как представить косинусоидальную волну, фаза которой сдвинулась на Δ? Конечно, как действительную часть F 0 exp [ i ((ω t -Δ 2)]; экспоненту в этом случае можно записать в виде exp[i(ωt-Δ)]=exp(iωt)exp( -iΔ). Алгебра экспонент гораздо легче алгебры синусов и косинусов; вот почему удобно использовать комплексные числа. Часто мы будем писать так:

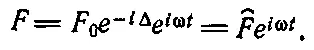(23.1)

Шляпка над буквой будет указывать, что мы имеем дело с комплексным числом, т. е.

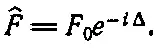
Однако пора начать решать уравнения, используя комплексные числа, тогда мы увидим, как надо применять комплексные числа в реальных обстоятельствах. Для начала попытаемся решить уравнение

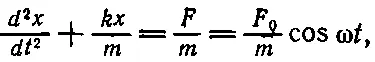(23.2)

где F — действующая на осциллятор сила, а х — его смещение. Хотя это и абсурдно, предположим, что х и F — комплексные числа. Тогда х состоит из действительной части и умноженной на i мнимой части; то же самое касается и F . Уравнение (23.2) в этом случае означает

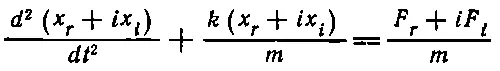
или

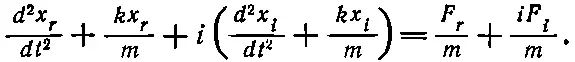
Комплексные числа равны, когда равны их действительные и мнимые части; следовательно, действительная, часть х удовлетворяет уравнению, в правой части которого стоит действительная часть силы . Оговорим с самого начала, что такое разделение действительных и мнимых частей возможно не всегда , а только в случае линейных уравнений, т. е. уравнений, содержащих х лишь в нулевой и первой степенях. Например, если бы уравнение содержало член λ х 2, то, сделав подстановку x r + ix i , мы получили бы λ( x r + ix i ) 2, и выделение действительной и мнимой частей привело бы нас к λ( х r 2- x i 2) и 2iλx rx i. Итак, мы видим, что действительная часть уравнения содержит в этом случае член -λ x i 2. Мы получили совсем не то уравнение, какое собирались решать.

Попытаемся применить наш метод к уже решенной задаче о вынужденных колебаниях осциллятора, т. е. об осцилляторе, на который действует внешняя сила. Как и раньше, мы хотим решить уравнение (23.2), но давайте начнем с уравнения

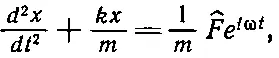(23.3)

где ^Fe i ω t — комплексное число. Конечно, х — тоже комплексное число, но запомним правило: чтобы найти интересующие нас величины, надо взять действительную часть х . Найдем решение (23.3), описывающее вынужденные колебания. О других решениях поговорим потом. Это решение имеет ту же частоту, что и внешняя (приложенная) сила. Колебание, кроме того, характеризуется амплитудой и фазой, поэтому если представить смещение числом ^ x , то модуль его скажет нам о размахе колебаний, а фаза комплексного числа — о временной задержке колебания. Воспользуемся теперь замечательным свойством экспоненты: (d/dt)[^ x exp( i ω t )]= i ω^ x exp( i ω t ). Дифференцируя экспоненциальную функцию, мы опускаем вниз экспоненту, делая ее простым множителем. Дифференцируя еще раз, мы снова приписываем такой же множитель, поэтому очень просто написать уравнение для ^ x : каждое дифференцирование по времени надо заменить умножением на iω. (Дифференцирование становится теперь столь же простым, как и умножение! Идея использовать экспоненциальные функции в линейных дифференциальных уравнениях почти столь же грандиозна, как изобретение логарифмов, которые заменили умножение сложением. Здесь дифференцирование заменяется умножением.) Таким образом, мы получаем уравнение

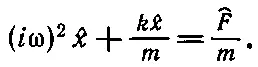(23.4)

[Мы опустили общий множитель e i ω t .] Смотрите, как все просто! Дифференциальное уравнение немедленно сводится к чисто алгебраическому; сразу же можно написать его решение

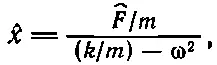
поскольку (iω) 2=-ω 2. Решение можно несколько упростить, подставив k/m=ω 2 0, тогда

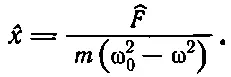(23.5)

Это, конечно, то же самое решение, которое уже было нами получено ранее. Поскольку m(ω 2 0-ω 2) — действительное число, то фазовые углы ^ F и ^ х совпадают (или отличаются на 180°, если (ω 2>ω 2 0). Об этом тоже уже говорилось. Модуль ^ х , который определяет размах колебаний, связан с модулем ^ F множителем 1/m(ω 2 0-ω 2); этот множитель становится очень большим, если ω приближается к ω 0. Таким образом, можно достичь очень сильного отклика, если приложить к осциллографу нужную частоту ω (если с нужной частотой толкать подвешенный на веревочке маятник, то он поднимается очень высоко).

Итак, мы можем решить задачу о колебательном движении, пользуясь изящной математикой. Однако изящество немногого стоит, когда задача и так решается просто; математику надо использовать тогда, когда решаются более сложные задачи. Перейдем поэтому к одной из таких задач, которая, кроме того, ближе к действительности, чем предыдущая. Из уравнения (23.5) следует, что, если ω в точности равна ω 0, амплитуда колебания становится бесконечной. Этого, конечно, не может быть, потому что многие вещи, например трение, ограничивают амплитуду, а мы их не учитывали. Изменим теперь (23.2) так, чтобы учесть трение.

Сделать это обычно довольно трудно, потому что силы трения очень сложны. Однако во многих случаях можно считать, что сила трения пропорциональна скорости движения объекта. Именно такое трение препятствует медленному движению тела в масле или другой вязкой жидкости. Когда предмет стоит на месте, на него не действуют никакие силы, но чем скорее он движется и чем быстрее масло должно обтекать этот предмет, тем больше сопротивление. Таким образом, мы предположим, что в (23.2), кроме уже написанных членов, существует еще один — сила сопротивления, пропорциональная скорости: F f =- c ( dx / dt ). Удобно записать с как произведение m на другую постоянную γ; это немного упростит уравнение.