Ричард Фейнман - Том 1. Механика, излучение и теплота

Итак, о трех элементах цепи. Первый называется емкостью (фиг. 23.4); в качестве примера емкости могут служить две металлические пластинки, разделенные тонким слоем диэлектрика.

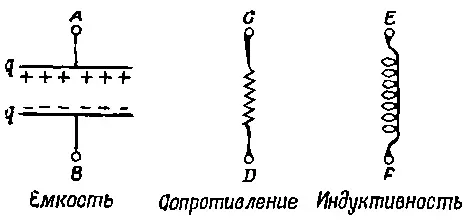
Фиг. 23.4. Три пассивных элемента цепи.

Если пластинки зарядить, то между ними возникает разность потенциалов. Та же самая разность потенциалов будет между точками А и В , потому что при любой дополнительной разности потенциалов вдоль соединительных проводов заряды стекут по проводам. Таким образом, заданной разности потенциалов V между пластинками соответствуют определенные заряды + q и - q на каждой пластинке. Между пластинками существует некое электрическое поле; мы даже вывели соответствующую формулу для него (см. гл. 13 и 14)

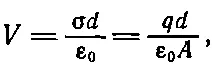(23.14)

где d — расстояние между пластинками, A — площадь пластинок. Заметим, что разность потенциалов линейно зависит от заряда. Если построить емкость не из параллельных пластин, а придать отдельным электродам какую-нибудь другую форму, разность потенциалов будет по-прежнему пропорциональна заряду, но постоянную пропорциональности не так-то легко будет рассчитать. Однако надо знать только одно: разность потенциалов между концами емкости пропорциональна заряду V = q / C ; множитель пропорциональности равен 1/ С ( С и есть емкость объекта).

Второй элемент цепи называется сопротивлением ; этот элемент оказывает сопротивление текущему через него электрическому току. Оказывается, что все металлические провода, а также многие другие материалы сопротивляются току одинаково; если к концам куска такого материала приложить разность потенциалов, то электрический ток в куске I = dq / dt будет пропорционален приложенной разности потенциалов

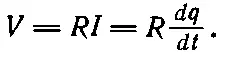(23.15)

Коэффициент пропорциональности называют сопротивлением R . Соотношение между током и разностью потенциалов вам, наверное, уже известно. Это закон Ома.

Если представлять себе заряд, сосредоточенный в емкости, как нечто аналогичное смещению механической системы х , то электрический ток dq / dt аналогичен скорости, сопротивление R аналогично коэффициенту сопротивления c , а 1/С аналогично постоянной упругости пружины k . Самое интересное во всем этом, что существует элемент цепи, аналогичный массе ! Это спираль, порождающая внутри себя магнитное поле, когда через нее проходит ток. Изменение магнитного поля порождает на концах спирали разность потенциалов, пропорциональную dI / dt . (Это свойство спирали используется в трансформаторах.) Магнитное поле пропорционально току, а наведенная разность потенциалов (так ее называют) пропорциональна скорости изменения тока

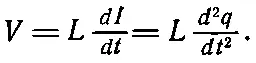(23.16)

Коэффициент L — это коэффициент самоиндукции ; он является электрическим аналогом массы.

Предположим, мы собираем цепь из трех последовательно соединенных элементов (фиг. 23.5); приложенная между точками 1 и 2 разность потенциалов заставит заряды двигаться по цепи, тогда на концах каждого элемента цепи тоже возникает разность потенциалов: на концах индуктивности V L = L ( d 2 q / dt 2), на сопротивлении V R = R ( dq / dt ), а на емкости V c = q / C .

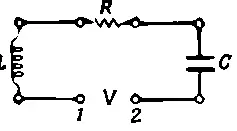
Фиг. 23.5. Электрический колебательный контур, состоящий из сопротивления, индуктивности и емкости.

Сумма этих напряжений дает нам полное напряжение

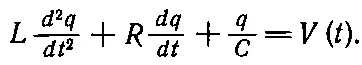(23.17)

Мы видим, что это уравнение в точности совпадает с механическим уравнением (23.6); будем решать его точно таким же способом. Предположим, что V ( t ) осциллирует; для этого надо соединить цепь с генератором синусоидальных колебаний. Тогда можно представить V ( t ) как комплексное число V , помня, что для определения настоящего напряжения V ( t ) это число надо еще умножить на exp ( i ω t ) и взять действительную часть. Аналогично можно подойти и к заряду q , а поэтому напишем уравнение, в точности повторяющее (23.8): вторая производная ^q— это (iω) 2^q, а первая — это ( i ω)^ q . Уравнение (23.17) перейдет в

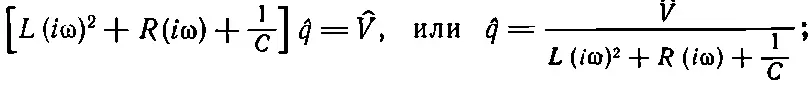
последнее равенство запишем в виде

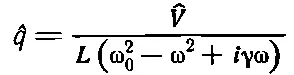(23.18)

где ω 2 0=1/ LC , а γ= R / L . Мы получили тот же знаменатель, что и в механической задаче, со всеми его резонансными свойствами! В табл. 23.1 приведен перечень аналогий между электрическими и механическими величинами.

Таблица 23.1 МЕХАНИЧЕСКИЕ И ЭЛЕКТРИЧЕСКИЕ ВЕЛИЧИНЫ

Еще одно чисто техническое замечание. В книгах по электричеству используют другие обозначения. (Очень часто в книгах на одну и ту же тему, написанных людьми разных специальностей, используются различные обозначения.) Во-первых, для обозначения √-1 используют букву j , а не i (через i должен обозначаться ток!). Во-вторых, инженеры предпочитают соотношение между ^ V и ^ I , а не между ^ V и ^ q . Они так больше привыкли. Поскольку ^I= d ^ q / dt = i ω^ q , то вместо ^ q можно подставить ^ I /iω, и тогда

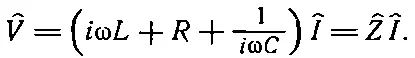(23.19)

Можно слегка изменить исходное дифференциальное уравнение (23.17), чтобы оно выглядело более привычно. В книгах часто попадается такое соотношение:

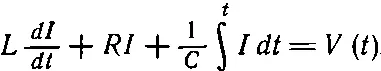(23.20)

Во всяком случае, мы находим, что соотношение (23.19) между напряжением ^ V и током ^ I то же самое, что и (23.18), и отличается только тем, что последнее делится на iω. Комплексное число R + i ω L +1/ i ω C инженеры-электрики часто называют особым именем: комплексный импеданс ^ Z . Введение новой буквы позволяет просто записать соотношение между током и сопротивлением в виде ^ V =^ Z ^ I . Объясняется это пристрастие инженеров тем, что в юности они изучали только цепи постоянного тока и знали только сопротивления и закон Ома: V = RI . Теперь они более образованы и имеют уже цепи переменного тока, но хотят, чтобы уравнения были те же самые. Вот они и пишут ^ V =^ Z ^ I , и единственная разница в том, что теперь сопротивление заменено более сложной вещью: комплексным числом. Они настаивают на том, что они не могут использовать принятого во всем мире обозначения для мнимой единицы и пишут j; поистине удивительно, что они не требуют, чтобы вместо буквы Z писали букву R ! (Много волнений доставляют им разговоры о плотности тока; ее они тоже обозначают буквой j. Сложности науки во многом связаны с трудностями в обозначениях, единицах и прочих выдумках человека, о чем сама природа и не подозревает.)