Ричард Фейнман - Том 1. Механика, излучение и теплота

На фиг. 23.8 изображена кривая поглощения — типично резонансная кривая.

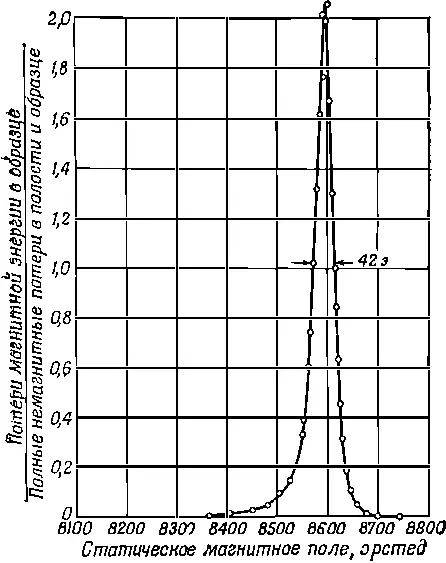
Фиг. 23.8. Зависимость потери, магнитной энергии в парамагнитном органическом соединении от напряженности приложенного поля.

Только получена она немного не так, как предыдущая. Частота горизонтального поля, управляющего колебаниями, все время остается постоянной, хотя, казалось бы, экспериментатор, чтобы получить кривую, должен менять частоту. Можно поступить и так, но технически легче оставить ω неизменной, а менять напряженность постоянного поля, что соответствует изменению ω 0в нашей формуле. Таким образом мы имеем дело с резонансной кривой для ω 0. Тем не менее мы получаем резонанс с определенными ω 0и γ.

Пойдем дальше. Следующий наш пример связан с атомным ядром. Движение протонов и нейтронов в ядре — в некотором смысле колебательное движение. Убедиться в этом можно при помощи такого эксперимента: давайте обстреливать ядра лития протонами. Мы обнаружим, что в ядрах при этом будут происходить какие-то реакции, в результате которых возникает γ-излучение. Кривая, изображающая количество испущенного излучения, имеет очень острый, типично резонансный максимум. Это изображено на фиг. 23.9.

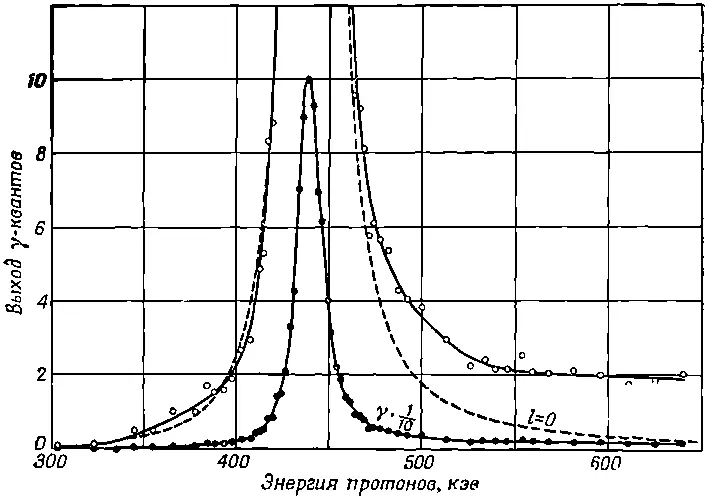
Фиг. 23.9. Зависимость интенсивности γ-излучения лития от энергии налетающих протонов. Пунктирная кривая —теоретическая, вычисленная для протонов с моментом количества движения l=0.

Однако приглядитесь к рисунку повнимательнее: на горизонтальной шкале отложена не частота, как обычно, а э нергия ! Дело в том, что та величина, которую в классической физике мы привыкли считать энергией, в квантовой механике оказывается определенным образом связанной с частотой некоторой волны. Если в привычной нам крупномасштабной физике при анализе какого-нибудь явления приходится иметь дело с частотой, то в квантовомеханических явлениях, связанных с атомным веществом, аналогичные кривые будут зависеть от энергии. Кривая на фиг. 23.9 иллюстрирует эту связь. Размышляя над этой кривой, можно прийти к мысли, что частота и энергия имеют глубокую взаимосвязь; так оно и есть на самом деле.

Вот еще одна резонансная кривая, полученная в результате опытов с атомными ядрами; она очень узкая, уже всех предыдущих. На фиг. 23.10 величина ω 0соответствует энергии 10 000 эв , а ширина γ равна приблизительно 10 -5эв; иначе говоря, Q=10 10!

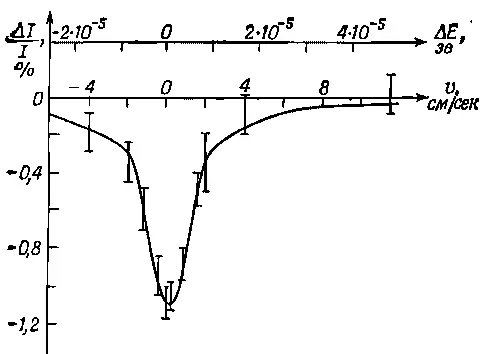
Фиг. 23.10. Кривая поглощения γ-излучения, полученная Р. Мёссбауэром.

Построив такую кривую, экспериментатор измерил Q самого добротного из ныне известных осцилляторов. Это проделал Р. Мёссбауэр, получивший за свои работы Нобелевскую премию. На горизонтальной шкале отложена скорость, потому что для сдвига частоты использовался эффект Допплера, получающийся в результате относительного движения источника и поглотителя. Цифры дают некоторое представление о тонкости эксперимента — пришлось измерять скорости в несколько сантиметров в секунду! Если продолжить горизонтальную шкалу влево, то нулевую частоту мы найдем на расстоянии 10 10 см ! Страницы для этого, пожалуй, не хватит!

Наконец, возьмем какой-нибудь выпуск журнала Physical Review, скажем, за 1 января 1962 г. Найдется ли в нем резонансная кривая? Резонансные кривые имеются непременно в каждом выпуске этого журнала, и на фиг. 23.11 изображена одна из таких кривых.

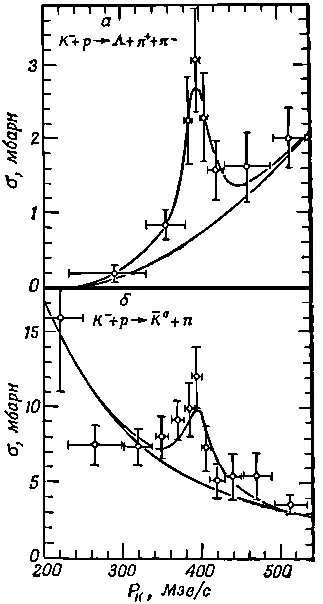
Фиг. 23.11. Зависимость эффективных сечений реакций от величины момента количества движения. а — K — +p→Λ+π + +π — ; б — K — +p→K 0 +n. Нижняя кривая описывает нерезонансный фон; верхняя кривая показывает, что на зтот фон наложено резонансное сечение.

Это очень интересная кривая. Она соответствует резонансу в реакциях со странными частицами (K --мезоны и протоны). Резонанс был обнаружен при измерении количества частиц разных сортов, получающихся в результате реакции. Разным продуктам реакции соответствуют разные кривые, но в каждой из них при одной и той же энергии есть пики примерно одинаковых очертаний. Значит, при определенной энергии K --мезона существует резонанс. При столкновении К --мезонов и протонов, наверное, создаются благоприятные для резонанса условия, а может быть, даже новая частица. Сегодня мы еще не можем сказать, что такое эти выбросы в кривых — «частица» или просто резонанс. Очень узкий резонанс соответствует очень точно отмеренному количеству энергии ; это бывает тогда, когда мы имеем дело с частицей. Когда резонансная кривая уширяется, то становится трудно сказать, с чем мы имеем дело — с частицей, которая живет очень мало, или просто с резонансом в реакции. В гл. 2 мы отнесли эти резонансы к частицам, но когда писалась та глава, об этом резонансе еще не было известно, поэтому нашу таблицу элементарных частиц можно дополнить!

Хотя глава названа «Переходные решения», речь здесь все еще в основном идет об осцилляторе, на который действует внешняя сила. Мы еще ничего не говорили об энергии колебаний. Давайте займемся ею.

Чему равна кинетическая энергия осциллятора? Она пропорциональна квадрату скорости. Здесь мы затронули важный вопрос. Предположим, что мы изучаем свойства некоторой величины А ; это может быть скорость или еще что-нибудь. Мы обратились к помощи комплексных чисел: A =^ Aexp (iωt), но в физике праведна и чтима только действительная часть комплексного числа. Поэтому если вам для чего-нибудь понадобится получить квадрат А , то не возводите в квадрат комплексное число, чтобы потом выделить его действительную часть.

Действительная часть квадрата комплексного числа не равна квадрату действительной части, она содержит еще и мнимую часть первоначального числа. Таким образом, если мы захотим найти энергию и посмотреть на ее превращения, нам придется на время забыть о комплексных числах.

Итак, истинно физическая величина А — это действительная часть A 0exp[i(ωt+Δ)], т. е. A = A 0соs(ωt+Δ), а комплексное число ^ А — это A 0exp(iΔ). Квадрат этой физической величины равен A 0 2cos 2(ωt+Δ). Он изменяется от нуля до максимума, как это предписывается квадратом косинуса. Максимальное значение квадрата косинуса равно 1, минимальное равно 0, а его среднее значение — это 1/ 2.