Ричард Фейнман - Том 1. Механика, излучение и теплота

Почему энергия электронов остается большой столь долгое время? Ведь с момента взрыва прошло уже 900 лет; как же получилось, что электроны крутятся все так же быстро? Причина такой продолжительности всего процесса в целом и сохранения электронами их большой энергии, в частности, до сих пор еще не совсем понятна.

Мы кратко расскажем еще об одном интересном эффекте, связанном с излучением быстродвижущейся частицы. По существу, этот процесс очень похож на только что описанное излучение. Предположим, что имеется материал, содержащий заряженные частицы и мимо пролетает очень быстрый электрон (фиг. 34.9).

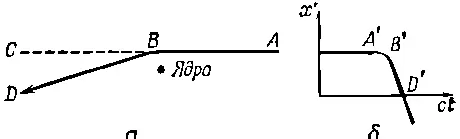
Фиг. 34.9. Быстрый электрон, пролетающий вблизи от ядра, излучает в направлении своего движения.

Тогда под действием электрического поля ядра электрон будет притягиваться и ускоряться, и на траектории появится изгиб. Чему будет равно излучение электрического поля в направлении С, если скорость электрона близка к скорости света? Вспомним наше правило: мы должны взять истинное движение, перенести его назад со скоростью с, и тогда мы получим кривую, производная которой определяет электрическое поле. Электрон примчался к нам со скоростью v, следовательно, при переносе получается обратное движение и вся траектория сожмется во столько раз, во сколько с—v меньше с. Таким образом, при 1-v/c≪1 кривизна кажущейся траектории в точке В' очень велика, и, взяв вторую производную, мы получаем мощное излучение в направлении движения. Следовательно, при прохождении через среду электроны большой энергии излучают вперед. Это явление называется тормозным излучением. На практике синхротроны используются не столько для получения электронов большой энергии (возможно, если бы их лучше умели выводить из синхротрона, мы бы этого не стали говорить), сколько для рождения энергичных фотонов, или γ~квантов в процессе прохождения электронов через плотные мишени, где они испускают тормозное излучение.

Рассмотрим теперь ряд других эффектов, связанных с движением источника. Пусть источник представляет собой покоящийся атом, колеблющийся со своей обычной частотой ω 0. Частота наблюдаемого света тогда будет равна ω 0. Но возьмем другой пример: пусть такой же атом колеблется с частотой ω 1и в то же время весь атом, весь осциллятор как целое движется со скоростью v по направлению к наблюдателю. Тогда истинное движение в пространстве будет таким, как изображено на фиг. 34.10,а.

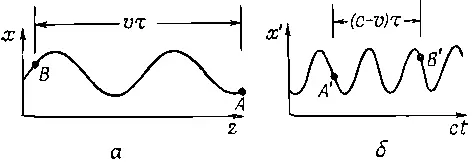
Фиг , 34.10. Движение осциллятора в плоскости х — z и в плоскости x '— t .

Используем наш обычный прием и добавим сτ, т. е. сместим всю кривую назад и получим колебания, представленные на фиг. 34.10,6. За промежуток времени τ осциллятор проходит расстояние vτ, а на графике с осями х' и у' соответствующее расстояние равно (с-v)τ. Таким образом, число колебаний с частотой ω 1, которое укладывалось в интервал Аτ, на новом чертеже укладывается теперь уже в интервал Δτ=(1-v/c) Δτ; осцилляции сжимаются, и, когда новая кривая будет двигаться мимо нас со скоростью с, мы увидим свет более высокой частоты, увеличенной за счет фактора сокращения (1-v/c). Итак, наблюдаемая частота равна

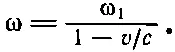(34.10)

Можно, конечно, объяснить этот эффект и другими способами. Пусть, например, тот же атом испускает не синусоидальную волну, а короткие импульсы (пип, пип, пип, пип) с некоторой частотой ω 1. С какой частотой мы будем их воспринимать? Первый импульс к нам придет спустя определенное время, а второй импульс придет уже через более короткое время, потому что атом за это время успел к нам приблизиться. Следовательно, промежуток времени между сигналами «пип» сократился за счет движения атома. Анализируя эту картину с геометрической точки зрения, мы придем к выводу, что частота импульсов увеличивается в 1/(1-v/c) раз.

Будет ли наблюдаться частота ω=ω 0/(1-v/c), если атом с собственной частотой ω 0движется со скоростью v к наблюдателю? Нет. Нам хорошо известно, что собственная частота движущегося атома ω 1и частота покоящегося атома ω 0— не одно и то же из-за релятивистского замедления хода времени. Так что если ω 0— собственная частота покоящегося атома, то частота движущегося атома будет равна

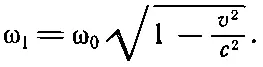(34.11)

Поэтому наблюдаемая частота ω окончательно равна

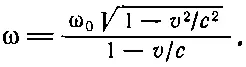(34.12)

Изменение частоты, возникающее в таком случае, называется эффектом Допплера: если излучающий объект движется на нас, излучаемый им свет кажется более синим, а если он движется от нас, свет становится более красным.

Приведем еще два других вывода этого интересного и важного результата. Пусть теперь покоящийся источник излучает с частотой ω 0, а наблюдатель движется со скоростью v к источнику. За время t наблюдатель сдвинется на новое расстояние vt от того места, где он был при t=0. Сколько радиан фазы пройдет перед наблюдателем? Прежде всего, как и мимо любой фиксированной точки, пройдет ω 0t, а также некоторая добавка за счет движения источника, а именно vtk 0(это есть число радиан на метр, умноженное на расстояние).

Отсюда число радиан за единицу времени, или наблюдаемая частота, равно ω 1=ω 0+k 0v. Весь этот вывод был произведен с точки зрения покоящегося наблюдателя; посмотрим, что увидит движущийся наблюдатель. Здесь мы снова должны учесть разницу в течении времени для наблюдателя в покое и движении, а это значит, что мы должны разделить результат на √( 1-v2/с 2). Итак, пусть k 0есть волновое число (количество радиан на метр в направлении движения), а ω 0— частота; тогда частота, регистрируемая движущимся наблюдателем, равна

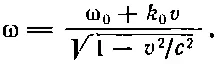(34.13)

Для света мы знаем, что k 0=ω 0/c. Следовательно, в рассматриваемом примере искомое соотношение имеет вид

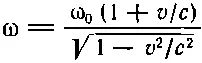(34.14)

и, казалось бы, не похоже на (34.12)!