Ричард Фейнман - Том 1. Механика, излучение и теплота

Мы, естественно, хотим описать поведение газа в масштабе, большем, чем длина свободного пробега, так что свойства газа не будут определяться поведением отдельных молекул. Например, смещение есть смещение центра инерции небольшого объема газа, а давление или плотность относятся к этому же объему. Мы обозначим давление через Р , а плотность через ρ, причем обе величины будут функциями от х и t . Необходимо помнить, что наше описание приближенное и справедливо лишь, когда свойства газа не слишком быстро меняются с расстоянием.

Итак, физические явления, происходящие в звуковой волне, обладают следующими тремя свойствами:

I. Газ движется, и плотность его меняется.

II. При изменении плотности меняется и давление.

III. Неравномерное распределение давления вызывает движение газа.

Рассмотрим сначала свойство II. Для любого газа, жидкости или твердого тела давление является функцией плотности. До прихода звуковой волны мы имели равновесное состояние с давлением Р 0и плотностью ρ 0. Давление Р зависит от плотности среды: Р=f(ρ), и в частности равновесное давление Р 0=f(ρ 0). Отклонения величины давления от равновесного в звуковой волне очень малы. Давление удобно измерять в барах (1 бар=10 5 н / м 2). Давление в одну стандартную атмосферу приблизительно равно 1 бар (1 атм=1,0133 бар ). Для звука обычно используется логарифмическая шкала интенсивности, так как восприятие уха, грубо говоря, растет логарифмически. В этой децибельной шкале уровень звукового давления I связан с амплитудой звукового давления:

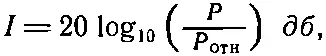(47.1)

где давление отнесено к некоторому стандартному давлению Р отн=2·10 -10 бар .

Звуковое давление Р=10 3Р отн=2·10 -7 бар [35] При таком выборе P отн Р — уже не максимальная амплитуда звукового давления, а «среднее квадратичное» давление, равное максимальному, деленному на 1/√2. соответствует довольно сильному звуку в 60 дб . Мы видим, что давление меняется в звуковой волне на очень малую величину по сравнению с равновесным или средним, равным 1 атм . Смещение и перепады плотности также очень малы. При взрывах, однако, изменения уже не столь малы; избыточное звуковое давление может превышать 1 атм . Такие большие перепады давления приводят к новым явлениям, которые мы рассмотрим позже. В звуковых волнах уровень силы звука выше 100 дб встречается редко; уровень силы звука в 120 дб уже вызывает боль в ушах. Поэтому, написав для звуковой волны

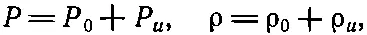(47.2)

можно считать, что изменение давления P u очень мало по сравнению с P 0, а изменение плотности ρ uочень мало по сравнению с ρ 0. Тогда

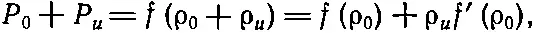(47.3)

где P 0=f(ρ 0) и f'(ρ 0) — производная от f(ρ), взятая при значении ρ=ρ 0. Второе равенство здесь возможно только потому, что ρ uочень мало. Таким образом, мы находим, что избыточное давление P u пропорционально избыточной плотности ρ u; коэффициент пропорциональности обозначается через ϰ:

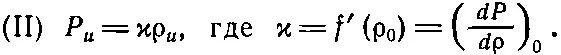
Это весьма простое соотношение и составляет точное содержание свойства II.

Перейдем теперь к свойству I. Предположим, что положение элемента объема воздуха, не возмущенного звуковой волной, есть х , а звук смещает его в момент времени t на величину χ( х,t ), так что его новое положение есть x+χ(x,t), как показано на фиг. 47.3.

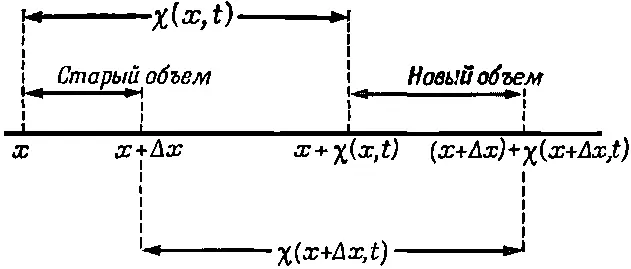
Фиг. 47.3. Смещение воздуха в точке х есть χ(х,t), а в точке х+Δх равно χ(x+Δx,t). Первоначальный объем, приходящийся на единицу площади в плоской звуковой волне, есть Δx, а окончательный объем равен Δx+χ(x+Δx,t)-χ(x,t).

Далее, положение соседнего элемента объема есть х +Δ х , и его смещенное положение есть х +Δ х +χ( х +Δ х,t ). Теперь можно найти изменение плотности. Поскольку мы рассматриваем плоскую волну, удобно взять единичную площадку, перпендикулярную оси х , т. е. направлению распространения волны. Количество воздуха, приходящееся на единичную площадку в интервале Δx, есть ρ 0Δx, где ρ 0— невозмущенная, или равновесная, плотность воздуха. Эта порция воздуха, смещенная звуковой волной, будет находиться теперь между x +χ( x,t ) и x+Δх+χ( х +Δ х,t ), причем количество воздуха в этом интервале то же самое, что в интервале Δx до прихода волны. Если через ρ обозначить новую плотность, то

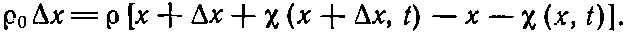(47.5)

Поскольку Δx мало, можно написать χ(x+Δx, t )-χ(x,t)=(∂χ/∂ x )Δx. Здесь уже появляется частная производная, потому что χ зависит и от x, и от времени. Наше уравнение принимает вид

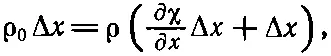(47.6)

или

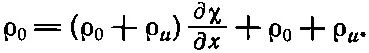(47.7)

Но в звуковой волне все изменения малы, так что ρ uмало, χ мало и ∂χ/∂ x тоже мало. Поэтому в уравнении, которое мы только что написали,

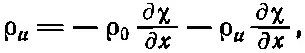(47.8)

можно пренебречь ρ u (∂χ/∂ x ) по сравнению с ρ 0(∂χ/∂ x ). Так мы приходим к соотношению, которое требовалось согласно свойству I:

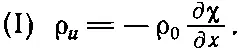(47.9)

Именно такой вид уравнения можно было ожидать из чисто физических соображений. Если смещение различно для разных х , плотность будет изменяться. Знак тоже правильный: если смещение χ растет с ростом х , так что воздух расширяется, плотность должна уменьшаться.

Теперь нам нужно найти третье уравнение — уравнение движения, производимого избытком давления. Зная соотношение между силой и давлением, можно получить уравнение движения. Возьмем объем воздуха толщиной Δ x и с единичной площадью грани, перпендикулярной х , тогда масса воздуха в этом объеме есть ρ 0Δ x , а ускорение воздуха есть ∂ 2χ/∂ t 2, так что масса, умноженная на ускорение для этого слоя, есть ρ 0Δx(∂ 2χ/∂t 2). (Если Δx мало, то безразлично, где брать ускорение — на краю слоя или где-нибудь посредине.) Сила, действующая на единичную площадку нашего слоя, перпендикулярную оси x, должна быть равна ρ 0Δx(∂ 2χ/∂t 2). В точке х мы имеем силу Р ( х,t ), действующую на единицу площади в направлении + х , а в точке x+Δx возникает сила в обратном направлении, по величине равная Р(x+Δx, t ) (фиг. 47.4):