Ричард Фейнман - Том 1. Механика, излучение и теплота
- Название:Том 1. Механика, излучение и теплота
- Автор:
- Жанр:
- Издательство:неизвестно
- Год:неизвестен
- ISBN:нет данных
- Рейтинг:
- Избранное:Добавить в избранное
-
Отзывы:
-
Ваша оценка:
Ричард Фейнман - Том 1. Механика, излучение и теплота краткое содержание
Том 1. Механика, излучение и теплота - читать онлайн бесплатно полную версию (весь текст целиком)
Интервал:
Закладка:
Итак, мы обнаруживаем, что сила в направлении х равна минус частной производной U по х :
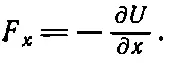 (14.11)
(14.11)
Точно так же и сила в направлении у получается дифференцированием U по у при постоянных х и z, а третья составляющая силы опять-таки есть производная по z при х и у постоянных:
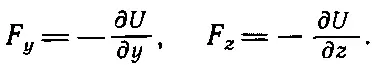 (14.12)
(14.12)
В этом и состоит способ получать силу из потенциальной энергии. Поле получается из потенциала в точности так же:
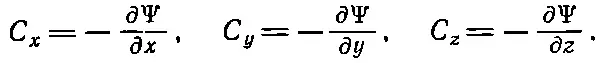 (14.13)
(14.13)
Заметим, кстати, что существует и другое обозначение (впрочем, пока оно нам не понадобится). Так как Сесть вектор с компонентами x, y, z , то символы ∂/∂ х , ∂/∂ y , ∂/∂ z , дающие х -, у -, z-компоненты поля, чем-то напоминают векторы. Математики изобрели знаменитый символ ∇, или grad, называемый «градиентом»; это не величина, а оператор, он делает из скаляра вектор. У него есть три составляющие: x-компонента этого grad есть ∂/∂ x , y-компонента — ∂/∂ y , а z-компонента — ∂/∂ z , и мы можем позабавиться, переписав наши формулы в виде
 (14.14)
(14.14)
Глядя на ∇; мы мгновенно узнаем, что наши уравнения векторные; но на самом деле уравнение (14.14) означает в точности то же, что и (14.11) и (14.12); просто это другой способ записи. Не желая писать каждый раз три уравнения, мы пишем одно лишь ∇ U .
Еще один пример полей и потенциалов связан с электричеством. В этом случае сила, действующая на неподвижное тело, равна заряду, умноженному на поле: F= q Е. (В x -составляющую силы входят, вообще говоря, и члены, которые зависят от магнитного поля. Но из уравнения (12.10) легко увидеть, что сила, действующая на частицу со стороны магнитных полей, всегда направлена поперек поля и поперек ее скорости. Благодаря этому свойству магнетизм не производит никакой работы над движущимся зарядом, потому что сила перпендикулярна перемещению. Значит, вычисляя кинетическую энергию в электрическом и магнитном полях, можно пренебречь вкладом магнитного поля, так как оно не изменяет кинетической энергии.) Положим, что имеется только электрическое поле. Тогда мы можем рассчитать энергию или произведенную работу точно таким же способом, как и для тяготения: вычислить величину φ, равную минус интегралу от Е· d sот произвольной фиксированной точки Р до точки, в которой вычисляется потенциал; тогда потенциальная энергия в электрическом поле равна просто произведению заряда на эту величину φ:
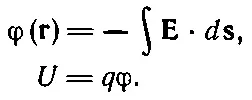
В качестве примера рассмотрим две параллельные металлические пластины с поверхностным зарядом ±σ (на единицу площади) каждая. Такая штука называется плоским конденсатором. Мы уж убедились раньше, что снаружи пластин сила равна нулю, а между ними существует постоянное электрическое поле. Оно направлено от плюса к минусу и равно σ/ε 0(фиг. 14.5).
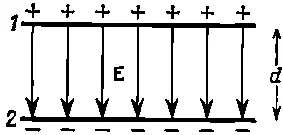
Фиг. 14.5. Поле между параллельными пластинами.
Мы хотим знать, какую работу надо совершить, чтобы перенести заряд от одной пластины к другой. Работа равна интегралу от (Сила.)·( d s). Его можно записать как произведение заряда на значение потенциала на пластине 1 минус та же величина на пластине 2:
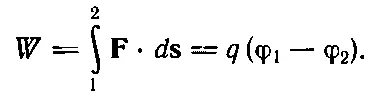
Интеграл здесь легко вычислить, так как сила постоянна, и если обозначить толщину конденсатора d , то интеграл равен
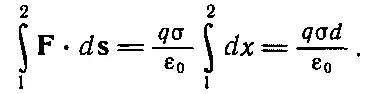
Разница в потенциалах Δφ=σ d /ε 0называется напряжением и φ измеряют в вольтах. Когда мы говорим, что пара пластин заряжена до определенного напряжения, мы хотим этим сказать, что разность электрических потенциалов двух пластин равна стольким-то вольтам. У конденсатора, сделанного из двух параллельных пластин с поверхностным зарядом ±σ, напряжение (или разность потенциалов этой пары пластин) равно σ d /ε 0.
ПРИЛОЖЕНИЕ
НЕКОТОРЫЕ ФИЗИЧЕСКИЕ ПОСТОЯННЫЕ
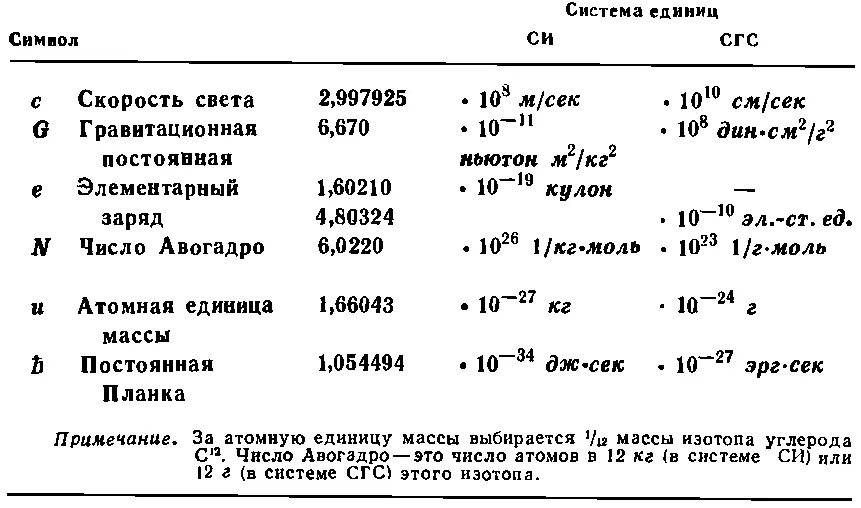
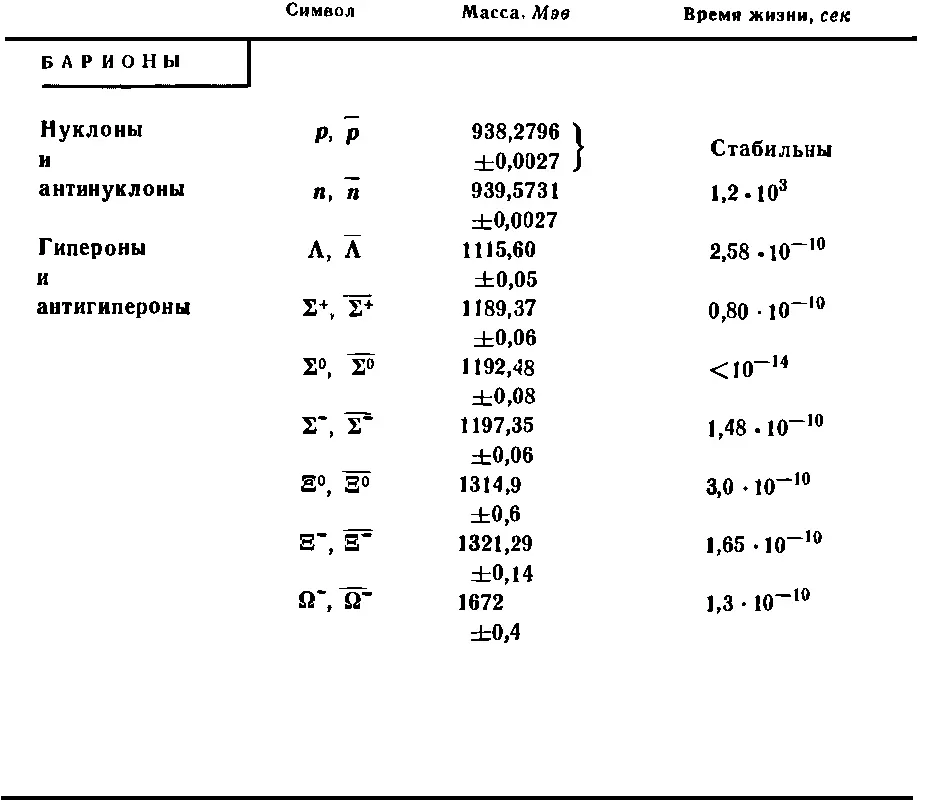
ЭЛЕМЕНТАРНЫЕ ЧАСТИЦЫ, ИХ МАССЫ
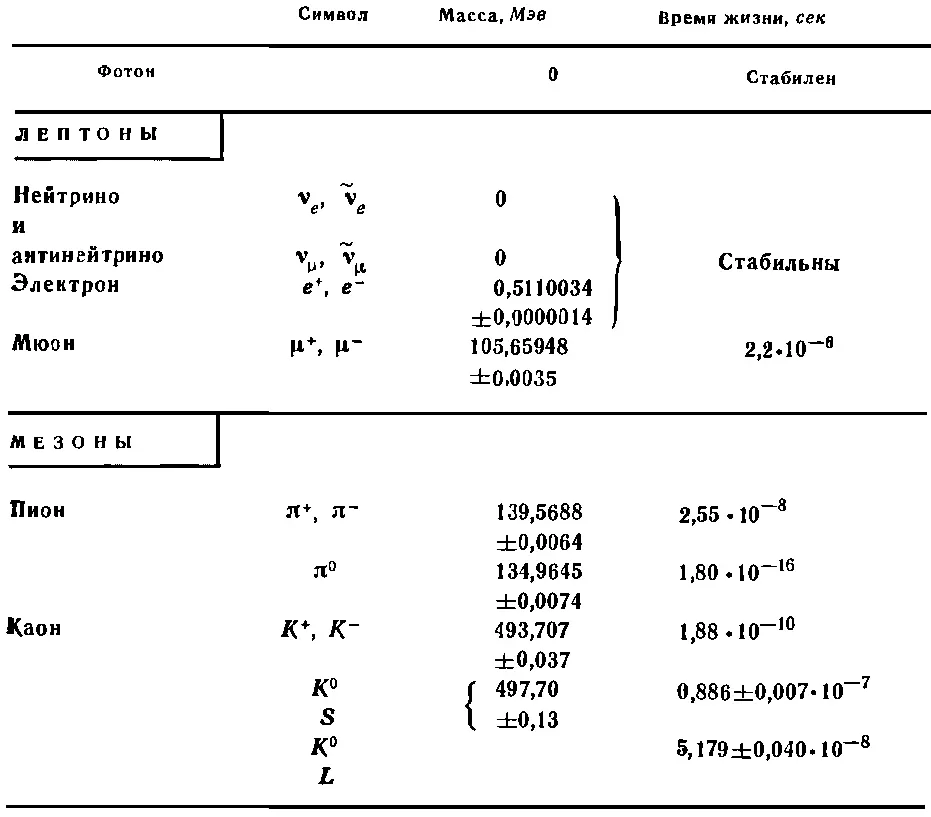
И ВРЕМЕНА ЖИЗНИ (ДАННЫЕ 1974. г)
Выпуск 2. Пространство. Время. Движение
Глава 15 СПЕЦИАЛЬНАЯ ТЕОРИЯ ОТНОСИТЕЛЬНОСТИ
§ 1. Принцип относительности
Свыше двухсот лет считалось, что уравнения движения, провозглашенные Ньютоном, правильно описывают природу. Потом в них была обнаружена ошибка. Обнаружена и тут же исправлена. И заметил ошибку, и исправил ее в 1905 г. один и тот же человек — Эйнштейн.
Второй закон Ньютона, выражаемый уравнением
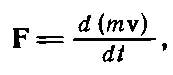
безмолвно предполагал, что m — величина постоянная. Но теперь мы знаем, что это не так, что масса тела возрастает со скоростью. В формуле, исправленной Эйнштейном, m появилась в таком виде:
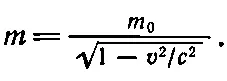 (15.1)
(15.1)
Здесь «масса покоя» m 0— это масса неподвижного тела, а c — скорость света (примерно 3·10 5 км / сек ).
Для кого теория нужна лишь для решения задач, тому этой формулы будет вполне достаточно. Больше ничего от теории относительности ему не понадобится; он просто введет в законы Ньютона поправку на изменяемость массы. Из самой формулы очевидно, что рост массы в обычных условиях незначителен.
Читать дальшеИнтервал:
Закладка:




