Ричард Фейнман - Том 2. Электромагнетизм и материя

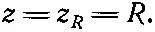(22.10)

Результаты наших рассуждений о трех сосредоточенных элементах цепи — индуктивности, емкости, сопротивлении — подытожены фиг. 22.4.

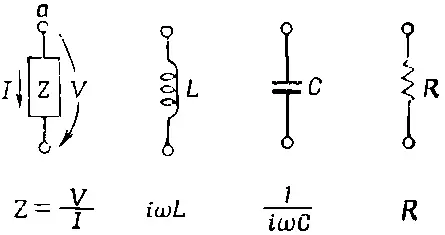
Фиг. 22.4. Идеальные сосредоточенные элементы цепи (пассивные).

На этом рисунке, как и на предыдущих, напряжение отмечено стрелкой, направленной от одной клеммы к другой. Если напряжение «положительно», т. е. если на клемме а потенциал выше , чем на клемме b , то стрелка указывает направление «падения напряжения».

Хотя мы сейчас говорим о переменных токах, конечно, можно включить сюда и особый случай цепей постоянного тока, если перейти к пределу, когда частота ω стремится к нулю. При нулевой частоте, т. е. при постоянном токе, импеданс индуктивности стремится к нулю; между клеммами наступает короткое замыкание. Импеданс же емкости при постоянном токе стремится к бесконечности; цепь между клеммами размыкается. Принимать в расчет при постоянных токах нужно только обычные сопротивления: они не зависят от частоты.

В описанных до сих пор элементах цепи ток и напряжение были пропорциональны друг другу. Если одно равно нулю, то и другое равно нулю. Обычно мы мыслим на таком языке: приложенное напряжение «ответственно» за ток или ток «создает» напряжение на клеммах. Элемент словно в некотором смысле «отвечает» на «приложенные» внешние условия. По этой причине такие элементы называются пассивными . Тем самым их можно противопоставить активным элементам, таким, как генераторы, которые мы рассмотрим в следующем параграфе и которые представляют собой источники колебаний токов или напряжений в цепи.

Поговорим теперь об активном элементе цепи, источнике и токов и напряжений в ней, т. е. о генераторе .

Пусть у нас имеется катушка, наподобие катушки самоиндукции, но только витков у нее немного и на магнитное поле ее собственного тока можно внимания не обращать. Эта катушка, однако, находится в переменном магнитном поле, подобном тому, какое создается вращающимся магнитом (фиг. 22.5).

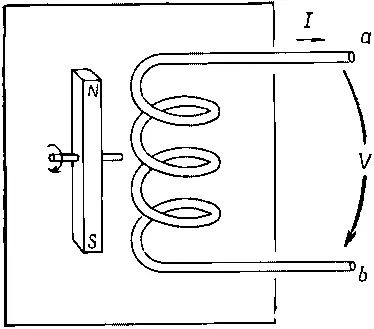
Фиг. 22.5. Генератор, состоящий из закрепленной катушки и вращающегося магнитного поля.

(Мы уже видели ранее, что такое вращающееся магнитное поле можно также создать с помощью подходящей совокупности катушек с переменными токами.) Сделаем снова несколько упрощающих допущений. Это все те же допущения, которые мы делали, говоря об индуктивности. В частности, мы предполагаем, что меняющееся магнитное поле ограничено лишь небольшой областью поблизости от катушки и за пределами генератора, в пространстве между клеммами, оно не чувствуется.

Повторяя опять в точности тот же анализ, что и для индуктивности, рассмотрим контурный интеграл от Евдоль замкнутой петли, которая начинается на зажиме а, проходит по катушке до зажима b и возвращается к началу по пространству между зажимами. Снова заключаем, что разность потенциалов между зажимами а и b равна всему интегралу от Евдоль петли:

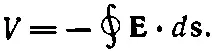
Этот контурный интеграл равен э.д.с. в цепи, и поэтому разность потенциалов V между выводами генератора тоже равна скорости изменения магнитного потока сквозь катушку:

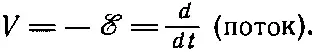(22.11)

Предполагается далее, что у идеального генератора магнитный поток через катушку определяется внешними условиями (такими, как угловая скорость вращающегося магнитного поля) и что на него никак не влияют токи, текущие через генератор. Таким образом, генератор (по крайней мере рассматриваемый нами идеальный ) — это не импеданс. Разность потенциалов на его зажимах определяется произвольно задаваемой э.д.с. ℰ( t ). Такой идеальный генератор представляют символом, показанным на фиг. 22.6.

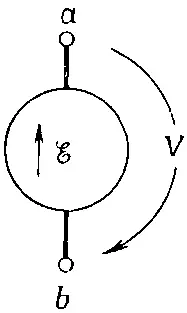
Фиг. 22.6. Обозначение идеального генератора.

Маленькая стрелка дает направление положительной э.д.с. Положительная э.д.с. в генераторе, изображенном на фиг. 22.6, создает напряжение V =ℰ с более высоким потенциалом на зажиме а .

Можно сделать генератор и по-другому. Внутри он будет устроен совершенно иначе, но снаружи, на зажимах, он ничем не будет отличаться от только что описанного. Представим катушку, которая вращается в неподвижном магнитном поле (фиг.22.7).

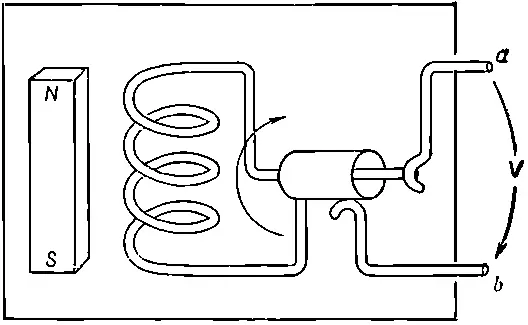
Фиг. 22.7. Генератор, состоящий из катушки, вращающейся в неподвижном магнитном поле.

Мы изобразили магнитную палочку, чтобы показать наличие магнитного поля, но его можно, конечно, заменить любым другим источником постоянного магнитного поля, скажем добавочной катушкой, по которой течет постоянный ток. Как показано на рисунке, вращающаяся катушка связана с внешним миром скользящими контактами, или «кольцами». Нас опять интересует разность потенциалов, которая появляется между клеммами а и b, т. е. интеграл от электрического поля между а и b по пути снаружи генератора.

Теперь в этой системе уже нет изменяющихся магнитных полей и на первый взгляд кажется удивительным, откуда на зажимах генератора берется напряжение. Действительно, ведь нигде же внутри генератора нет никаких электрических полей. Мы, как обычно, предполагаем для наших идеальных элементов, что внутри них провода сделаны из идеально проводящего материала; а, как уже неоднократно повторялось, электрическое поле внутри идеального проводника равно нулю. Но это не всегда верно. Это неверно тогда, когда проводник движется в магнитном поле. Правильное утверждение таково: общая сила , действующая на произвольный заряд внутри идеального проводника, должна быть равна нулю. Иначе в нем возник бы бесконечный ток свободных зарядов. Так что надо брать сумму электрического поля Еи векторного произведения скорости проводника vна магнитное поле В; это есть полная сила, действующая на единичный заряд, и вот она-то всегда равна нулю:

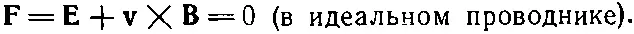(22.12)