Ричард Фейнман - Том 2. Электромагнетизм и материя

Однако бывают совсем простые схемы, которые этим методом не проанализируешь. Например, схема фиг. 22.13.

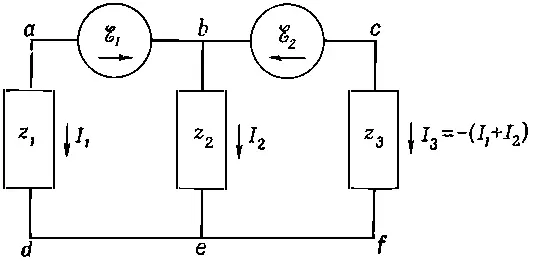
Фиг. 22,13. Цепь, которую нельзя проанализировать с помощью последовательных и параллельных комбинаций.

Чтобы проанализировать эту цепь, надо расписать уравнения для токов и напряжений по правилам Кирхгофа. Давайте проделаем это. Имеется только одно уравнение для токов:

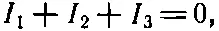
откуда

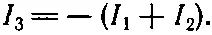
Выкладки можно сэкономить, если этот результат сразу же подставить в уравнения для напряжений. В этой схеме таких уравнений два:

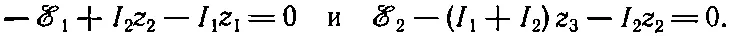
На два уравнения приходится два неизвестных тока. Решая их, получаем I 1и I 2:

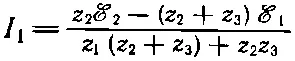(22.20)

и

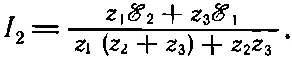(22.21)

А третий ток получается как сумма первых двух.

Вот еще пример цепи, которую по правилам параллельных и последовательных импедансов рассчитывать нельзя (фиг. 22.14).

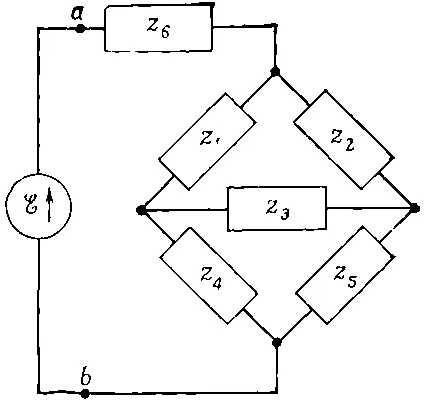
Фиг. 22.14. Мостиковая схема.

Такую схему называют «мостик». Она встречается во многих приборах, измеряющих импедансы. В таких схемах обычно интересуются таким вопросом: как должны соотноситься различные импедансы, чтобы ток через импеданс z s был равен нулю? Вам предоставляется право найти те условия, при которых это действительно так.

Положим, мы подключили генератор ℰ к цепи, в которой есть множество сложных переплетений импедансов (схематически это показано на фиг. 22.15, а ).

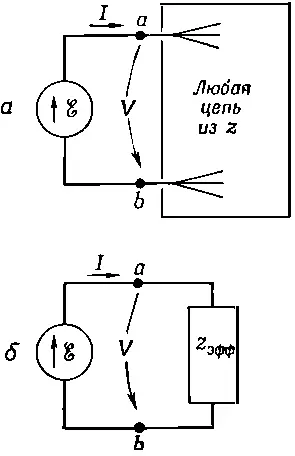
Фиг. 22.15. Любая сеть пассивных элементов с двумя выводами эквивалентна эффективному импедансу.

Все уравнения, вытекающие из правил Кирхгофа, линейны, и поэтому, вычислив из них ток I через генераторы, мы получим величину I, пропорциональную ℰ. Можно написать

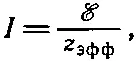
где теперь z эфф— это некоторое комплексное число, алгебраическая функция всех элементов цепи. (Если в цепи нет никаких генераторов, кроме упомянутого, то в формуле не будет добавочной части, не зависящей от ℰ.) Но получившееся уравнение — это как раз то, которое нужно было бы написать для схемы фиг. 22.15, б . И покуда нас интересует только то, что происходит слева от зажимов а и b, до тех пор обе схемы фиг. 22.15 эквивалентны . И поэтому можно сделать общее утверждение, что любую цепь пассивных элементов с двумя выводами можно заменить одним-единственным импедансом z эфф , не изменив в остальной части цепи ни токов, ни напряжений. Утверждение это, естественно, всего лишь мелкое замечание о том, что следует из правил Кирхгофа, а в конечном счете — из линейности уравнений Максвелла.

Идею эту можно обобщить на схемы, в которые входят как генераторы, так и импедансы. Представьте, что мы глядим на эту схему «с точки зрения» одного из импедансов, который мы обозначим z n(фиг. 22.16, а ).

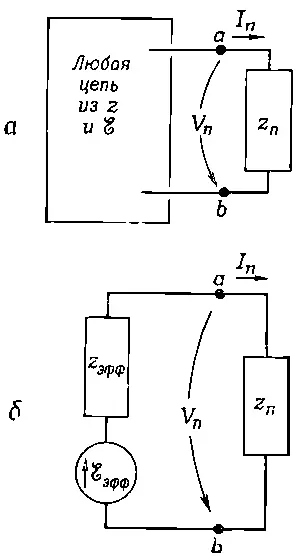
Фиг. 22.16. Любую сеть с двумя выводами можно заменить генератором, последовательно соединенным с импедансом.

Если бы решить уравнение для тока, мы бы увидели, что напряжение V n между зажимами а и b есть линейная функция I, которую можно записать в виде

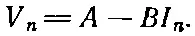(22.22)

Здесь А и В зависят от генераторов и импедансов в цепи слева от зажимов. Например, в схеме, показанной на фиг. 22.13, мы находим V 1= I 1 z 1. Это можно переписать [используя (22.20)] в виде

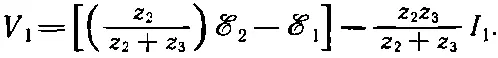(22.23)

Тогда полное решение мы получаем, комбинируя это уравнение с уравнением для импеданса z 1т. е. с V 1=I 1z 1, или в общем случае комбинируя (22.22) с

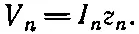
Если мы рассмотрим теперь случай, когда z nподключается к простой цепи из последовательно соединенных генератора и импеданса (см. фиг. 22.15, б), то уравнение, соответствующее (22.22), примет вид

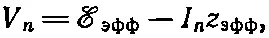
что совпадает с (22.22), если принять ℰ эфф=A и z эфф=B. Значит, если нас интересует лишь то, что происходит направо от выводов а и b, то произвольную схему фиг. 22.16 можно всегда заменить эквивалентным сочетанием генератора, последовательно соединенного с импедансом.

Мы видели, что для создания в индуктивности тока I надо из внешней цепи доставить энергию U= 1/ 2LI 2. Когда ток спадает до нуля, эта энергия уводится обратно во внешнюю цепь.

В идеальной индуктивности механизма потерь энергии нет. Когда через индуктивность течет переменный ток, энергия перетекает то туда, то сюда — от индуктивности к остальной части цепи и обратно, но средняя скорость, с какой энергия передается в цепь, равна нулю. Мы говорим, что индуктивность — недиссипативный элемент, в ней не растрачивается (не «диссипирует») электрическая энергия.

Точно так же возвращается во внешнюю цепь и энергия конденсатора U= 1/ 2СV 2, когда он разряжается. Когда он стоит в цепи переменного тока, то энергия течет то в него, то из него, но полный поток энергии за каждый цикл равен нулю. Идеальный конденсатор — тоже недиссипативный элемент.

Мы знаем, что э. д. с.— это источник энергии. Когда ток I течет в направлении э.д.с., то энергия поставляется во внешнюю цепь со скоростью dU/dt=ℰI. Если электричество гонят против э.д.с. (с помощью других генераторов), то э. д. с. поглощает энергию со скоростью ℰI; поскольку I отрицательно, то и dU/dt отрицательно.