Ричард Фейнман - Том 2. Электромагнетизм и материя

Если генератор подключен к сопротивлению R, то ток через сопротивление равен I=ℰ/R. Энергия, поставляемая генератором со скоростью ℰI, поглощается сопротивлением. Эта энергия тратится на нагрев сопротивления и для электрической энергии цепи фактически уже потеряна. Мы говорим, что электрическая энергия рассеивается, диссипирует в сопротивлении. Скорость, с какой она рассеивается, равна dU/dt=RI 2.

В цепи переменного тока средняя скорость потерь энергии в сопротивлении — это среднее значение RI 2за цикл. Поскольку I=^Ie iωt(что, собственно, означает, что I меняется как cosωt), то среднее значение I 2за цикл равно |^I| 2/2, потому что ток в максимуме — это |^I|, а среднее значение cos 2ωt равно 1/ 2.

А что можно сказать о потерях энергии, когда генератор подключен к произвольному импедансу z ? (Под «потерями» мы, конечно, понимаем превращение электрической энергии в тепловую.) Всякий импеданс z может быть разбит на действительную и мнимую части, т. е.

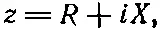(22.24)

где R и X — числа действительные. С точки зрения эквивалентных схем можно сказать, что всякий импеданс эквивалентен сопротивлению, последовательно соединенному с чисто мнимым импедансом, называемым реактансом (фиг. 22.17).

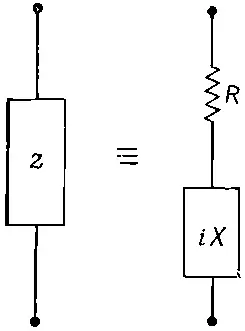
Фиг. 22.17. Любой импеданс эквивалентен последовательному соединению чистого сопротивления и чистого реактанса.

Мы уже видели раньше, что любая цепь, содержащая только L и C, обладает импедансом, выражаемым чисто мнимым числом. А раз в любом из L и С в среднем никаких потерь не бывает, то и в чистом реактансе, в котором имеются только L и С, потерь энергии не бывает. Можно показать, что это должно быть верно для всякого реактанса.

Если генератор с э. д. с. ℰ подсоединен к импедансу z (см. фиг. 22.17), то его э. д. с. должна быть связана с током I из генератора соотношением

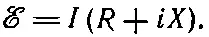(22.25)

Чтобы найти, с какой средней скоростью подводится энергия, нужно усреднить произведение ℰI. Но теперь следует быть осторожным. Оперируя с такими произведениями, надо иметь дело только с действительными величинами ℰ(t) и I(t). (Действительные части комплексных функций изображают настоящие физические величины только тогда, когда уравнения линейны; сейчас же речь идет о произведении, а это, несомненно, вещь нелинейная.)

Пусть мы начали отсчитывать t так, что амплитуда ^I оказалась действительным числом, скажем I 0; тогда истинное изменение I во времени дается формулой

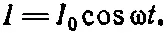
Входящая в уравнение (22.25) э.д.с. — это действительная часть от

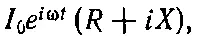
или

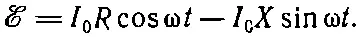(22.26)

Два слагаемых в (22.26) представляют падение напряжений на R и X (см. фиг. 22.17). Мы видим, что падение напряжения на сопротивлении находится в фазе с током, тогда как падение напряжения на чисто реактивной части находится с током в противофазе .

Средняя скорость потерь энергии <���Р> ср, текущей от генератора, есть интеграл от произведения ℰI за один цикл, деленный на период Т ; иными словами,

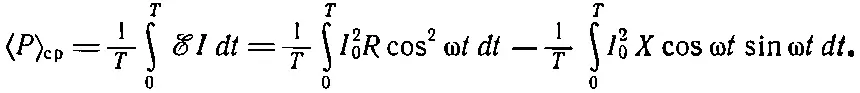
Первый интеграл равен 1/ 2 I 0 2 R , а второй равен нулю. Стало быть, средняя потеря энергии в импедансе z = R + iX зависит лишь от действительной части z и равна I 0 2 R /2. Это согласуется с нашим прежним выводом о потерях энергии в сопротивлении. В реактивной части потерь энергии не бывает.

А теперь мы рассмотрим интереснейшую цепь, которую можно выражать через параллельные и последовательные сочетания. Начнем с цепи, изображенной на фиг. 22.18, а .

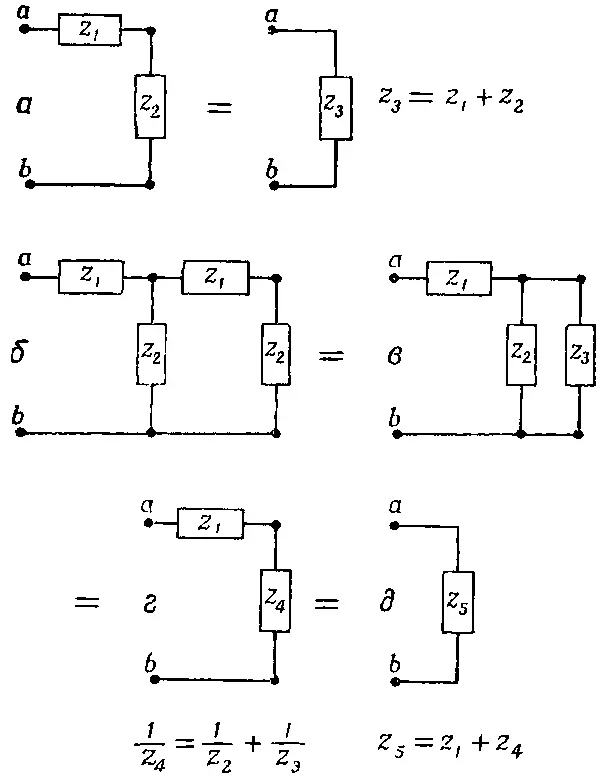
Фиг. 22.18. Эффективный импеданс лестницы.

Сразу видно, что импеданс между зажимами а и b просто равен z 1+z 2. Возьмем теперь цепь потруднее (фиг. 22.18, б ). Ее можно проанализировать с помощью правил Кирхгофа, но нетрудно обойтись и последовательными и параллельными комбинациями. Два импеданса на правом конце можно заменить одним z 3=z 1+z 2(см. фиг. 22.18, в). Тогда два импеданса z 2и z 3можно заменить их эквивалентным параллельным импедансом z 4(фиг. 22.18, г). И наконец, z 1и z 4эквивалентны одному импедансу z 5(фиг. 22.18, д ).

А теперь можно поставить забавный вопрос: что произойдет, если к цепи, показанной на фиг. 22.18, б, бесконечно подключать все новые и новые звенья (штриховая линия на фиг. 22.19, а)?

Фиг. 22.19. Эффективный импеданс бесконечной лестницы.

Можно ли решить задачу о такой бесконечной цепи? Представьте, это совсем не трудно. Прежде всего мы замечаем, что такая бесконечная цепь не меняется, если новое звено подключить к «переднему» концу. Ведь если к бесконечной цепи добавляется одно звено, она остается все той же бесконечной цепью. Пусть мы обозначили импеданс между зажимами а и b бесконечной цепи через z 0; тогда импеданс всего того, что справа от зажимов с и d , тоже равен z 0. Поэтому если смотреть с переднего конца, то вся цепь представляется в виде, показанном на фиг. 22.19, б . Заменяя два параллельных импеданса z 2и z 0одним и складывая его с z 1, сразу же получаем импеданс всего сочетания

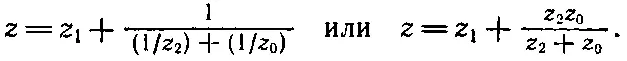
Но этот импеданс тоже равен z 0. Получается уравнение

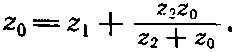
Найдем из него z 0:

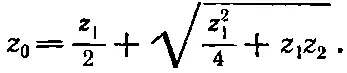(22.27)

Таким образом, мы нашли решение для импеданса бесконечной лестницы повторяющихся параллельных и последовательных импедансов. Импеданс z 0называется характеристическим импедансом такой бесконечной цепи.