Ричард Фейнман - Том 2. Электромагнетизм и материя

А наше прежнее утверждение о том, что внутри идеальных проводников электрических полей не бывает, верно лишь тогда, когда скорость проводника vравна нулю; в противном случае справедливо выражение (22.12).

Вернемся к нашему генератору, показанному на фиг. 22.7. Теперь мы видим, что контурный интеграл от электрического поля Емежду зажимами а и b по проводящим путям генератора должен быть равен контурному интегралу от v× Bпо тому же пути;

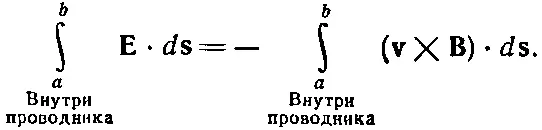
Однако по-прежнему остается верным, что контурный интеграл от Епо замкнутой петле, включая возвращение от зажима b к а вне генератора, должен быть равен нулю, потому что меняющиеся магнитные поля отсутствуют. Так что первый интеграл в (22.13) по-прежнему равен V — напряжению на зажимах. Оказывается, что интеграл в правой части (22.13) просто равен быстроте изменения потока через катушку, а значит, по правилу потока, равен э.д.с. катушки. И опять получается, что разность потенциалов между зажимами равна э.д.с. цепи в согласии с уравнением (22.11). Так что все равно, какой у нас генератор: меняется ли в нем магнитное поле возле закрепленной катушки, вертится ли в закрепленном магнитном поле катушка,— внешние свойства генераторов одни и те же. На клеммах всегда существует напряжение V , которое не зависит от тока в цепи, а определяется только условиями внутри генератора, формируемыми по нашему произволу.

Поскольку мы пытаемся понять работу генератора, основываясь на уравнениях Максвелла, может возникнуть вопрос об обычном химическом элементе, о батарейке для карманного фонарика. Это тоже генератор, т. е. источник напряжения, хотя и применяется он только в цепях постоянного тока. Проще всего разобраться в элементе, изображенном на фиг. 22.8.

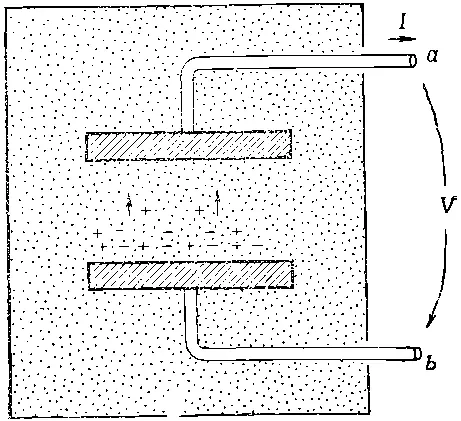
Фиг. 22.8. Химический элемент.

Представьте две металлические пластинки, погруженные в какой-то химический раствор. Пусть раствор содержит в себе положительные и отрицательные ионы. Мы предположим еще, что ионы одного сорта, скажем отрицательные, много массивнее ионов, имеющих противоположную полярность, так что их движение в растворе (диффузия) происходит намного медленнее. Наконец, положим, что тем или иным способом удалось добиться изменения концентрации раствора от места к месту, так что число ионов обеих полярностей, скажем у нижней пластинки, становится намного больше концентрации ионов у верхней пластинки. Благодаря большей подвижности положительные ионы легче проникнут в область низких концентраций, так что будет наблюдаться легкий избыток положительных зарядов, достигающих верхней пластинки. Она зарядится положительно, а нижняя будет обладать избытком отрицательного заряда. По мере того как все больше и больше зарядов диффундирует к верхней пластинке, потенциал ее будет расти, пока возникающее между пластинками электрическое поле не создаст силу, действующую на ионы, которая компенсирует их избыточную подвижность. Два электрода быстро достигают разности потенциалов, характерной для внутреннего устройства этого элемента.

Рассуждая так же, как это мы делали, когда говорили об идеальном конденсаторе, мы убедимся, что, если нет избытка диффузии ионов какого-либо знака, разность потенциалов между зажимами а и b равна просто контурному интегралу от электрического поля между электродами. Конечно, между конденсатором и таким химическим элементом есть существенная разница. Если на мгновение закоротить выводы конденсатора, он разрядится и разности потенциалов между выводами уже не будет. В случае же химического элемента ток с зажимов можно снимать непрерывно, никак не изменяя при этом э.д.с., пока, конечно, реактивы в элементе не израсходуются. Известно, что в реальном элементе разность потенциалов на зажимах убывает по мере возрастания снимаемого с него тока. Но при нашей идеализации задачи легко себе представить, что у нас есть идеальный элемент, в котором напряжение на электродах не зависит от силы тока. Тогда реальный элемент можно рассматривать как идеальный, соединенный последовательно с сопротивлением.

Как мы видели в предыдущем параграфе, очень просто описывать идеальные элементы схем, говоря лишь о том, что происходит вне элемента. Ток и напряжение связаны линейно. Но очень сложно описать все то, что на самом деле происходит внутри элемента, и весьма трудно при этом пользоваться языком уравнений Максвелла. Представьте, что вам нужно точно описать электрические и магнитные поля внутри радиоприемника, состоящего из сотен сопротивлений, емкостей и самоиндукций. Было бы непосильным делом проанализировать такую мешанину, пользуясь уравнениями Максвелла. Но, делая множество приближений, которые мы описали в § 2, и переводя существенные черты реальных элементов схем на язык идеализации, можно проанализировать электрическую цепь сравнительно просто. Сейчас мы покажем, как это делается. Пусть имеется цепь, которая состоит из генератора и нескольких импедансов, между собой так, как показано на фиг. 22.9.

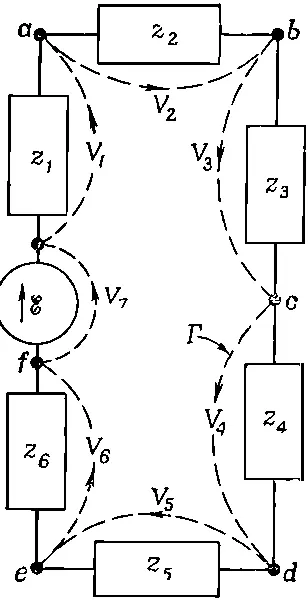
Фиг. 22.9. Сумма падений напряжения вдоль любого замкнутого пути равна нулю.

Согласно нашим приближениям, в областях между отдельными элементами цепи магнитного поля нет. Поэтому интеграл от Евдоль любой кривой, которая не проходит ни через один из элементов, равен нулю. Рассмотрим кривую Г, показанную штрихом на фиг. 22.9, которая обходит по цепи кругом. Контурный интеграл от Евдоль этой кривой состоит из нескольких частей. Каждая часть — это интеграл от одного зажима элемента цепи до следующего. Мы назвали этот контурный интеграл падением напряжения на элементе цепи. Тогда весь контурный интеграл равен просто сумме падений напряжения на всех элементах цепи порознь:

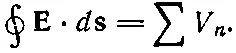
А поскольку контурный интеграл равен нулю, то получается, что сумма разностей потенциалов вдоль всего замкнутого контура цепи равна нулю:

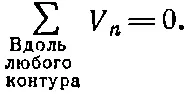(22.14)

Этот результат следует из одного из уравнений Максвелла, утверждающего, что в области, где нет магнитных полей, криволинейный интеграл от Епо замкнутому контуру равен нулю. Теперь рассмотрим другую цепь (фиг. 22.10).