Ричард Фейнман - Том 2. Электромагнетизм и материя

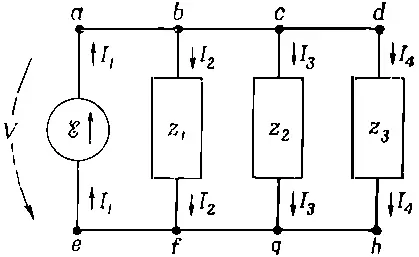
Фиг, 22.10. Сумма токов, входящих в любой узел, равна нулю .

Горизонтальная линия, соединяющая выводы а, b, с и d , нарисована для того, чтобы показать, что эти выводы все связаны между собой или что они соединяются проводами с ничтожным сопротивлением. Во всяком случае такой чертеж означает, что все выводы а, b, с, d находятся под одним потенциалом, а выводы е, f, g и h — тоже под одним. Тогда падение напряжения V на любом из четырех элементов одинаковое.

Но одна из наших идеализации состояла в том, что на выводах импедансов сосредоточиваются пренебрежимо малые количества электричества. Предположим теперь, что и электрическим зарядом, накапливаемым на соединительных проводах, тоже можно пренебречь. Тогда сохранение заряда требует, чтобы любой заряд, покинувший один из элементов цепи, немедленно входил в какой-либо другой элемент цепи. Или, что то же самое, чтобы алгебраическая сумма токов, входящих в любую из точек соединения, была равна нулю. Под точкой соединения мы понимаем любую совокупность выводов, таких, как а, b , с, d , которые соединены друг с другом. Такая совокупность соединенных между собой выводов обычно называется «узлом». Сохранение заряда, стало быть, требует, чтобы в цепи, показанной на фиг. 22.10, было

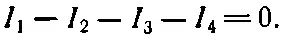(22.15)

Сумма токов, входящих в узел, состоящий из четырех выводов е, f, g, h , тоже должна быть равна нулю:

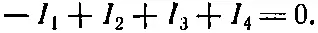(22.16)

Ясно, что это то же самое уравнение, что и (22.15). Оба эти уравнения не независимы. Общее правило гласит, что сумма токов, втекающих в любой узел, обязана быть равна нулю :

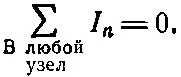(22.17)

Наше прежнее заключение о том, что сумма падений напряжений вдоль замкнутого контура равна нулю, должно выполняться для каждого контура сложной цепи. Точно так же наш результат, что сумма сил токов, втекающих в узел, равна нулю, тоже должен выполняться для любого узла. Эти два уравнения известны под названием правил Кирхгофа . С их помощью можно найти силы токов и напряжения в какой угодно цепи.

Рассмотрим, например, цепь посложнее (фиг. 22.11).

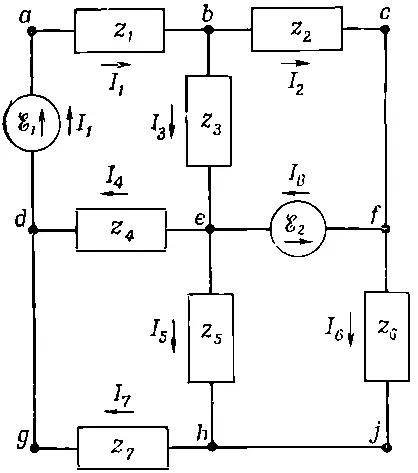
Фиг. 22.11. Анализ цепи с помощью правил Кирхгофа.

Как определить токи и напряжения в ней? Прямой путь решения таков. Рассмотрим каждый из четырех вспомогательных контуров цепи. (Скажем, один контур проходит через клеммы а, b, е, d и обратно к а.) Для каждого замкнутого контура напишем уравнение первого правила Кирхгофа — сумма падений напряжения вдоль всякого контура равна нулю. Нужно помнить, что падение напряжения считается положительным, если направление обхода совпадает с направлением тока, и отрицательным, если направление обхода противоположно направлению тока; и надо еще помнить, что падение напряжения на генераторе равно отрицательному значению э.д.с. в этом направлении. Так что для контура abeda получается

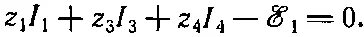
Прилагая те же правила к остальным контурам, получим еще три сходных уравнения.

После этого нужно написать уравнения для токов в каждом узле цепи. Например, складывая все токи в узле b, получаем

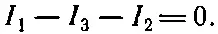
Аналогично, в узле е уравнение для токов принимает вид

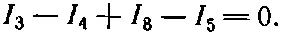
В изображенной схеме таких уравнений для токов пять. Оказывается, однако, что любое из этих уравнений можно вывести из остальных четырех, поэтому независимых уравнений только четыре. Итого в нашем распоряжении восемь независимых линейных уравнений: четыре для напряжений, четыре для токов. Из них можно получить восемь независимых токов. А если станут известны токи, то определится и вся цепь. Падение напряжения на любом элементе дается током через этот элемент, умноженным на его импеданс (а для источников напряжения они вообще известны заранее).

Мы видели, что одно из уравнений для тока зависит от остальных. Вообще-то уравнений для напряжения тоже можно написать больше, чем нужно. Хотя в схеме фиг. 22.11 и рассматривалась только четверка самых маленьких контуров, но ничего не стоило взять другие контуры и выписать для них уравнения для напряжений. Можно было взять, скажем, путь abcfeda . Или сделать обход по пути abcfehgda . Вы видите, что контуров — множество. И, анализируя сложные схемы, ничего не стоит получить слишком много уравнений. Но хоть есть правила, которые подсказывают, как надо поступать, чтобы вышло наименьшее количество уравнений, обычно и так бывает сразу понятно, как выписать нужное число простейших уравнений. Кроме того, одно-два лишних уравнения вреда не приносят. К неверному ответу они не приведут, разве только немного запутают выкладки.

В гл. 25 (вып. 2) мы показали, что, если два импеданса z 1и z 2соединены последовательно , они эквивалентны одиночному импедансу z s, равному

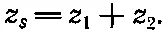(22.18)

Кроме того, было показано, что, когда два импеданса соединены параллельно , они эквивалентны одиночному импедансу z p, равному

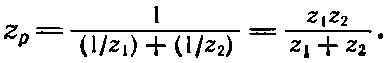(22.19)

Если вы теперь оглянетесь назад, то увидите, что, выводя эти результаты, на самом деле вы пользовались правилами Кирхгофа. Часто можно проанализировать сложную схему, повторно применяя формулы для последовательного и параллельного импедансов. Скажем, таким способом можно проанализировать схему, показанную на фиг. 22.12.

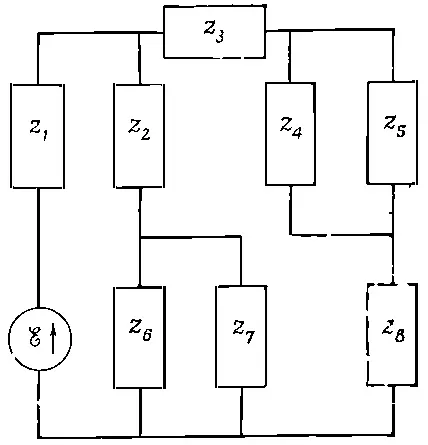
Фиг. 22.12. Цепь, которую можно проанализировать с помощью последовательных и параллельных комбинаций.

Импедансы z 4и z 5можно заменить их параллельным эквивалентом, то же можно сделать с импедансами z 6и z 7. Затем импеданс z 2можно скомбинировать с параллельным эквивалентом z 6и z 7по правилу последовательного соединения импедансов. Так постепенно можно свести всю схему к генератору, последовательно соединенному с одним импедансом Z . И тогда ток через генератор просто равен ℰ/ Z . А действуя в обратном порядке, можно найти токи в каждом импедансе.