Ричард Фейнман - Том 2. Электромагнетизм и материя

Рассмотрим теперь частный пример, когда последовательный элемент — всегда индуктивность L , а шунтовой элемент — емкость С (фиг. 22.20, а ).

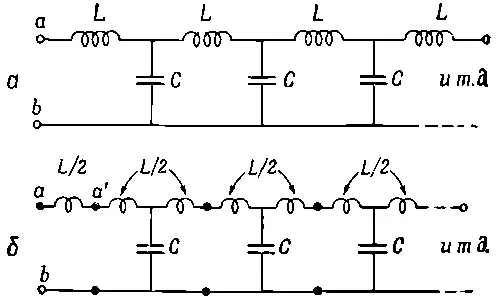
Фиг. 22.20. Лестница L—C, изображенная двумя эквивалентными способами.

В этом случае импеданс бесконечной сети получается, если положить z 1=iωL и z 2=1/ i ω С . Заметьте, что первое слагаемое z 1/2 в (22.27) равно просто половине импеданса первого элемента. Естественнее было бы поэтому (или по крайней мере проще) рисовать нашу бесконечную сеть так, как показано на фиг. 22.20, б . Глядя на бесконечную сеть из зажима a ', мы бы увидали характеристический импеданс

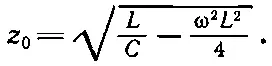(22.28)

Смотря по тому, какова частота ω, наблюдаются два интересных случая. Если ω 2меньше 4/LC, то второе слагаемое под корнем меньше первого, и импеданс z 0станет действительным числом. Если же ω 2больше 4/LС, то импеданс z 0станет чисто мнимым числом и его можно записать в виде

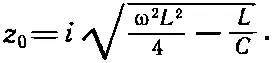
Раньше мы сказали, что цепь, составленная из одних только мнимых импедансов, таких, как индуктивности и емкости, будет иметь чисто мнимый импеданс. Но как же тогда выходит, что в той цепи, которую мы сейчас рассматриваем (а в ней есть только одни L и С ), импеданс при частотах ниже √(4/LC) представляет собой чистое сопротивление? Для высоких частот импеданс чисто мнимый, в полном согласии с нашим прежним утверждением. Для низких же частот импеданс — чистое сопротивление и поэтому поглощает энергию. Но как может цепь, подобно сопротивлению, непрерывно поглощать энергию, если она составлена только из индуктивностей и емкостей? Ответ состоит в том, что этих емкостей и самоиндукций бесконечное множество, и получается, что, когда источник соединен с цепью, он обязан сперва снабдить энергией первую индуктивность и емкость, затем вторую, третью и т. д. В цепях подобного рода энергия непрерывно и с постоянной скоростью отсасывается из генератора и безостановочно течет в цепь. Энергия запасается в индуктивностях и емкостях вдоль цепи.

Эта идея подсказывает интересную мысль о том, что фактически происходит внутри цепи. Следует ожидать, что если к переднему концу цепи подключить источник, то действие этого источника начнет распространяться вдоль по цепи к бесконечному концу. Распространение волн вдоль линии очень похоже на излучение от антенны, которая отбирает энергию от питающего ее источника; точнее, можно ожидать, что такое распространение происходит, когда импеданс действителен, т. е. когда ω меньше √(4/LC). Но когда импеданс чисто мнимый, т. е. при ω, больших √4/LC, то такого распространения ожидать не следует.

В предыдущем параграфе мы видели, что бесконечная лестничная сеть (см. фиг. 22.20) непрерывно поглощает энергию, если эта энергия подводится с частотой, которая ниже некоторого критического значения √(4/LC), называемого граничной частотой ω 0. У нас возникла мысль, что этот эффект можно понять, основываясь на представлении о непрерывном переносе энергии вдоль линии. С другой стороны, на высоких частотах (при ω >ω 0) непрерывного поглощения энергии не бывает; тогда следует ожидать, что токи, видимо, не смогут «проникнуть» далеко вдоль линии. Поглядим, верны ли эти представления.

Пусть передний конец лестницы соединен с каким-то генератором переменного тока, и нас интересует, как выглядит напряжение, скажем, в 754-м звене лестницы. Поскольку сеть бесконечна, при переходе от одного звена к другому происходит всегда одно и то же; так что можно просто посмотреть, что случается, когда мы переходим от n-го звена к (n+1)-му. Токи I nи напряжения V nмы определим так, как показано на фиг. 22.21, а .

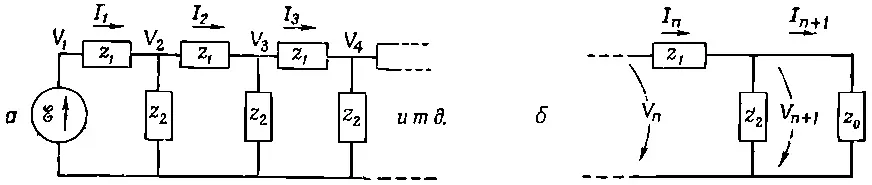
Фиг. 22.21. Нахождение фактора распространения лестницы.

Напряжение V n +1можно получить из V n , если вспомнить, что остаток лестницы (за n-м звеном) всегда можно заменить ее характеристическим импедансом z 0; и тогда достаточно проанализировать только схему фиг. 22.21, б. Мы прежде всего замечаем, что каждое V n , поскольку это напряжение на зажимах сопротивления z 0, должно быть равно I n z 0. Кроме того, разность между V n и V n +1равна просто I n z 1:

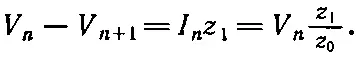
Получается отношение

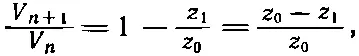
которое можно назвать фактором распространения для одного звена лестницы; обозначим его α. Для всех звеньев

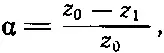(22.29)

и напряжение за n - м звеном равно

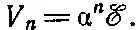
Теперь ничего не стоит найти напряжение за 754-м звеном; оно просто равно произведению ℰ на 754-ю степень α.

Как выглядит α для лестницы L —С на фиг. 22.20, а ? Взяв z 0из уравнения (22.27) и z 1= i ω L , получим

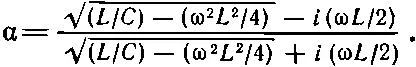
Если частота на входе ниже граничной частоты ω 0=√(4/ LС ), то корень — число действительное, и модули комплексных чисел в числителе и знаменателе одинаковы. Поэтому значение α по модулю равно единице; можно написать

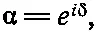
а это означает, что величина (модуль) напряжения в каждом звене одна и та же; меняется только фаза. Она меняется на число δ; оно на самом деле отрицательно и представляет собой «задержку» напряжения по мере того, как последнее проходит по сети. А для частот выше граничной частоты ω 0лучше вынести в числителе и знаменателе (22.31) множитель i и переписать его в виде

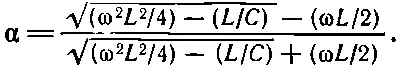(22.32)

Теперь фактор распространения α — число действительное , притом меньшее единицы . Это означает, что напряжение в некотором звене всегда меньше напряжения в предыдущем звене; множитель пропорциональности равен α. При частотах выше ω 0напряжение быстро спадает по мере движения вдоль сети. Кривая модуля α как функции частоты похожа на график, приведенный на фиг. 22.22.