Ричард Фейнман - Том 2. Электромагнетизм и материя

Другим неверным утверждением в теории «сухой» воды является предположение, которое мы делали при рассмотрении потока на границе между ним и поверхностью твердого предмета. Когда мы обсуждали обтекание потоком цилиндра (например, фиг. 40.11), то считали, что жидкость скользит по поверхности твердого тела. В нашей теории скорость на поверхности твердого тела могла иметь любое значение, зависящее от того, как началось движение, и мы не учитывали никакого «трения» между жидкостью и твердым телом. Однако то, что скорость реальной жидкости должна на поверхности твердого тела сходить на нуль, — экспериментальный факт. Следовательно, наши решения для цилиндра и с циркуляцией, и без нее неправильны, как и результат о создании вихря. О более правильных теориях я расскажу вам в следующей главе.

В предыдущей главе мы говорили о поведении воды, пренебрегая при этом эффектами вязкости. Теперь же мне хотелось бы обсудить, как вязкость влияет на течение жидкости. Рассмотрим реальное поведение жидкости. Я опишу качественно, как ведет себя жидкость в самых разных условиях, так чтобы вы получше прочувствовали эту науку. И хотя вы увидите сложные уравнения и услышите о трудных вещах, наша цель совсем не в том, чтобы изучить все тонкости. Цель этой главы скорее «общеобразовательная», просто я хочу дать вам некоторое понятие о том, как устроен мир. Однако здесь все же есть один пункт, который стоит того, чтобы его выучить: полезно знать простое определение вязкости. С него мы и начнем. Все же остальное предназначено для вашего удовольствия.

В предыдущей главе мы нашли, что законы движения жидкости содержатся в уравнении

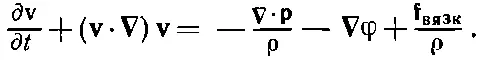(41.1)

В нашем приближении «сухой» воды мы отбрасывали последнее слагаемое, так что всеми эффектами вязкости мы пренебрегали. Кроме того, мы иногда делали еще дополнительное приближение, считая жидкость несжимаемой, и при этом получали дополнительное уравнение:

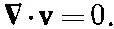
Это приближение часто оказывается вполне приличным, особенно когда скорость потока много меньше скорости звука. Но в реальных жидкостях мы почти никогда не можем пренебречь внутренним трением, называемым нами вязкостью; большинство интересных вещей в поведении жидкости так или иначе связано именно с этим свойством. Так, мы узнали, что циркуляция «сухой» воды никогда не изменяется: если ее не было вначале, то она никогда и не появится. Но в то же время мы повседневно сталкиваемся с циркуляцией в жидкости. Так что нашу теорию надо подправить.

Начнем с важного экспериментального факта. Когда мы занимались потоком «сухой» воды, обтекающей какой-то предмет или текущей мимо него, т. е. так называемым «потенциальным потоком», у нас не было причин запретить воде иметь составляющую скорости, тангенциальную к поверхности предмета; только нормальная компонента должна была быть равна нулю. Мы не принимали во внимание возможность возникновения сил сдвига между жидкостью и твердым телом. А вот оказывается, хотя это далеко и не очевидно, что во всех случаях, где это было проверено экспериментально, скорость жидкости на поверхности твердого тела в точности равна нулю . Вы замечали, конечно, что лопасти вентилятора собирают на себя тонкий слой пыли, и это несмотря на то, что они вращаются в воздухе. Тот же эффект можно наблюдать даже в больших аэродинамических трубах. Почему же пыль не сдувается воздухом? Несмотря на то что лопасти вентилятора быстро вращаются в воздухе, скорость воздуха относительно них, измеренная непосредственно на их поверхности, равна нулю, так что поток воздуха не возмущает даже мельчайших пылинок [60] Большие частицы можно сдуть со стола, а мельчайшие— невозможно. Их верхушки не «высовываются» в поток. . Мы должны модифицировать теорию так, чтобы она согласовалась с тем экспериментальным фактом, что во всех обычных жидкостях молекулы, находящиеся рядом с поверхностью, имеют нулевую скорость (относительно поверхности [61] Можно представить себе и такой случай, когда это окажется неверным. Теоретически стекло есть тоже «жидкость», однако оно вполне может скользить по стальной поверхности. Так что и такая теория где-то должна погореть. ).

Сначала мы характеризовали жидкость так, что если приложить к ней напряжение сдвига, то, сколь бы мало оно ни было, жидкость «поддается» и течет. В статическом случае никаких напряжений сдвига нет. Однако, когда равновесия еще нет, в момент, когда вы давите на жидкость, силы сдвига вполне могут быть. Вязкость как раз и описывает эти силы, возникающие в движущейся жидкости. Чтобы измерить силы сдвига в процессе движения жидкости, рассмотрим такой эксперимент. Предположим, что имеются две плоские твердые пластины, между которыми находится вода (фиг. 41.1), причем одна из пластин неподвижна, тогда как другая движется параллельно ей с малой скоростью v 0.

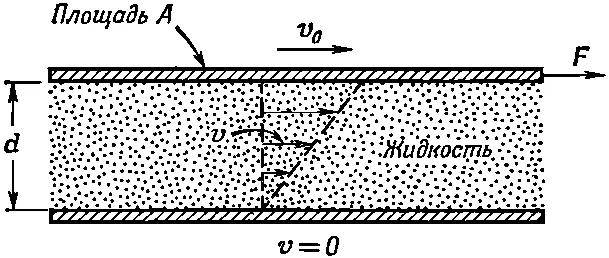
Фиг. 41.1. Увлечение жидкости между двумя параллельными пластинками.

Если вы будете измерять силу, требуемую для поддержания движения верхней пластины, то найдете, что она пропорциональна площади пластины и отношению v 0/ d , где d — расстояние между пластинами. Таким образом, напряжение сдвига F / A пропорционально v 0/ d :

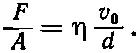
Коэффициент пропорциональности η называется коэффициентом вязкости .

Если перед нами более сложный случай, то мы всегда можем рассмотреть в воде небольшой плоский прямоугольный объем, грани которого параллельны потоку (фиг. 41.2).

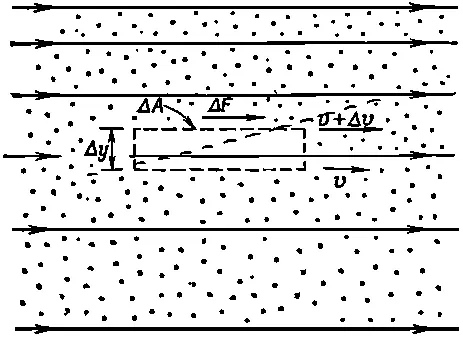
Фиг. 41.2. Напряжения сдвига в вязкой жидкости.

Силы в этом объеме определяются выражением

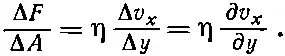(41.2)

Далее, ∂ v x /∂ y представляет скорость изменения деформаций сдвига, определенных нами в гл. 38, так что силы в жидкости пропорциональны скорости изменения деформаций сдвига.