Ричард Фейнман - Том 2. Электромагнетизм и материя

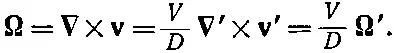(41.21)

А наше основное уравнение (41.17) перейдет в

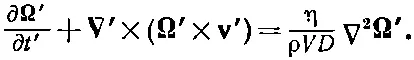
Все постоянные при этом собираются в один множитель, который мы, следуя традиции, обозначим через 1/ℛ:

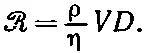(41.22)

Если теперь мы просто запомним, что все наши уравнения должны выписываться для величин, измеряемых в новых единицах, то все штрихи можно опустить. Тогда уравнения для потока примут вид

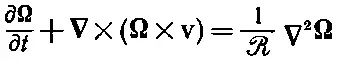(41.23)

и

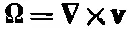
с условиями,

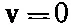
для

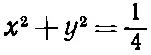(41.24)

и

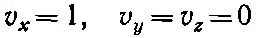
для

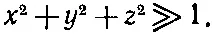
Что все это значит? Если, например, мы решили задачу для потока с одной скоростью V 1и некоторого цилиндра диаметром D 1, а затем интересуемся обтеканием цилиндра другого диаметра D 2другой жидкостью, то поток будет одним и тем же при такой скорости V 2, которая отвечает тому же самому числу Рейнольдса, т. е. когда

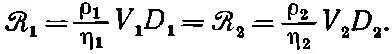(41.25)

В любых случаях, когда числа Рейнольдса одинаковы, поток при выборе надлежащего масштаба х ', у ', z ' и t ' будет «выглядеть» одинаково. Это очень важное утверждение, ибо оно означает, что мы можем определить поведение потока воздуха при обтекании крыла самолета, не строя самого самолета и не испытывая его. Вместо этого мы можем сделать модель и провести измерения, используя скорость, которая дает то же самое число Рейнольдса. Именно этот принцип позволяет нам применять результаты измерений над маленькой моделью самолета в аэродинамической трубе или результаты, полученные с моделью корабля, к настоящим объектам. Напомню, однако, что это можно делать только при условии, что сжимаемостью жидкости можно пренебречь. В противном случае войдет новая величина — скорость звука. При этом различные модели будут действительно соответствовать друг другу только тогда, когда отношение V к скорости звука тоже приблизительно одинаково. Отношение скорости V к скорости звука называется числом Маха . Таким образом, для скоростей, близких к скорости звука или больших, поток в двух задачах будет выглядеть одинаково, если и число Маха и число Рейнольдса в обеих ситуациях одинаковы .

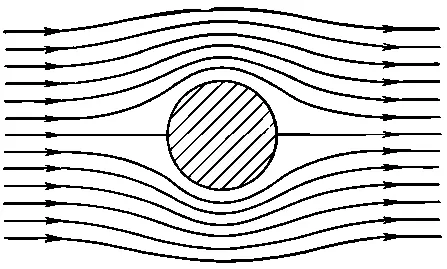
Вернемся теперь обратно к задаче об обтекании цилиндра медленным (почти несжимаемым) потоком. Я дам вам качественное описание потока реальной жидкости. О таком потоке нам необходимо знать множество вещей. Например, какая увлекающая сила действует на цилиндр? Сила, увлекающая цилиндр, показана на фиг. 41.4 как функция величины ℛ, которая пропорциональна скорости V , если все остальное фиксировано.

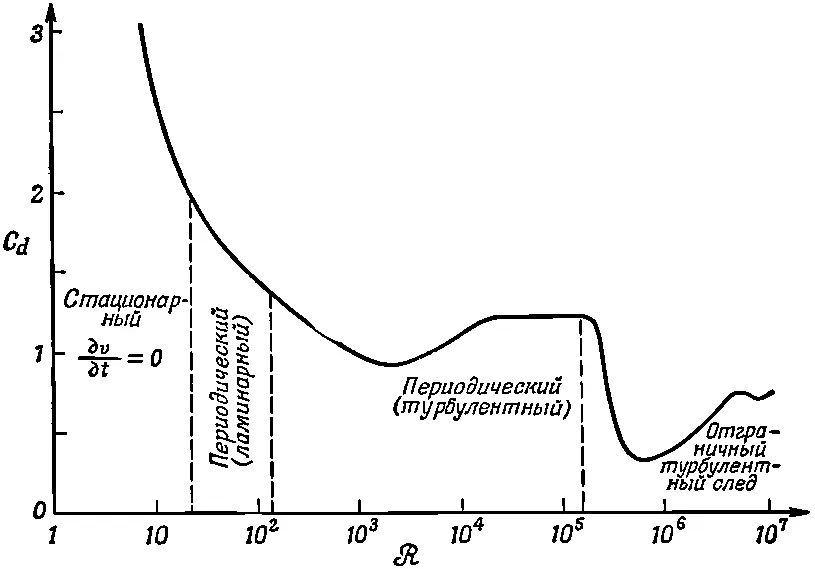
Фиг. 41.4. Коэффициент увлечения С d кругового цилиндра как функция числа Рейнольдса.

Фактически на рисунке отложен коэффициент увлечения С d — безразмерное число, равное отношению силы к 1/ 2ρ V 2 Dl ( d — диаметр, l —длина цилиндра, а ρ —плотность жидкости):

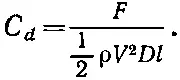
Коэффициент увлечения изменяется довольно сложным образом, как бы намекая нам на то, что в потоке происходит нечто интересное и сложное. Свойства потока полезно описывать для различных областей изменения числа Рейнольдса. Прежде всего, когда число Рейнольдса очень мало, поток вполне стационарен, скорость в любой точке потока постоянна и он плавно обтекает цилиндр. Однако распределение линий потока не похоже на их распределение в потенциальном потоке. Они описывают решение несколько другого уравнения. Когда скорость очень мала или, что эквивалентно, вязкость очень велика, так что вещество по своей консистенции напоминает мед, можно отбросить инерционные члены и описать поток уравнением

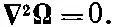
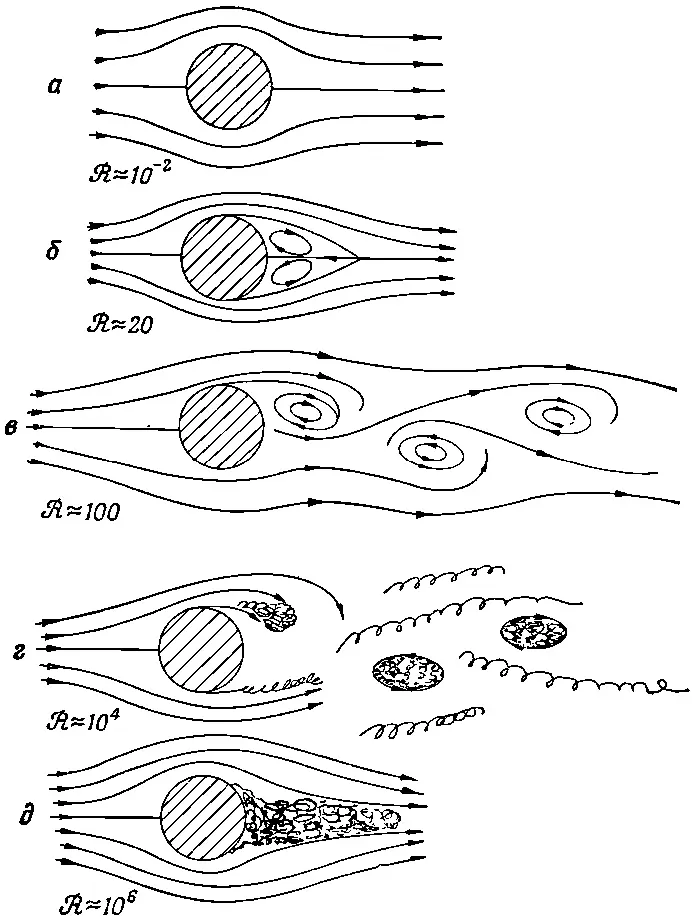
Это уравнение впервые было решено Стоксом. Он также решил задачу для сферы. Когда маленькая сфера движется при малых числах Рейнольдса, то к ней приложена сила, равная 6πηaV, где а — радиус сферы, а V — его скорость.

Это очень полезная формула: она говорит нам о скорости, с которой мельчайшие частички, которые приближенно можно считать шариками, движутся в жидкости под действием данной силы, как, например, в центрифуге, или при осаждении, или, наконец, в процессе диффузии. В области малых чисел Рейнольдса, т. е. при ℛ<1, линии v вокруг цилиндра имеют такой вид, как на фиг. 41.5.

Фиг. 41.5. Вязкий поток вблизи цилиндра (малая вязкость).

Если теперь мы увеличим скорость потока, так что число Рейнольдса станет несколько больше единицы, то увидим, что поток изменится.

Фиг. 41.6. Поток, обтекающий цилиндр, при различных числах Рейнольдса.

Как показано на фиг. 41.6, б , за сферой возникнут вихри. До сих пор неясно, существовали ли вихри и при малых числах Рейнольдса или же они возникли неожиданно при некотором определенном числе? Обычно считали, что циркуляция нарастает постепенно. Однако теперь думают, что скорее она проявляется неожиданно и возрастает с увеличением ℛ. Во всяком случае, поток в районе от ℛ=10 до ℛ=30 меняет свой характер. За цилиндром образуется пара вихрей.