Ричард Фейнман - Том 2. Электромагнетизм и материя

В общем случае мы пишем

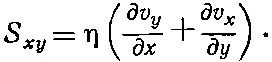(41.3)

При равномерном вращении жидкости производная ∂ v х /∂ у равна ∂ v y /∂ x с обратным знаком, а S xy будет равна нулю, как это и требуется, ибо в равномерно вращающейся жидкости напряжения отсутствуют. (Подобную же вещь мы проделывали в гл. 39 при определении е xy .) Разумеется, для S yz и S zx тоже есть соответствующие выражения.

В качестве примера применения этих идей рассмотрим движение жидкости между двумя коаксиальными цилиндрами. Пусть радиус внутреннего цилиндра равен а , его скорость будет v а, а радиус внешнего цилиндра пусть будет b, а скорость равна v b (фиг. 41.3).

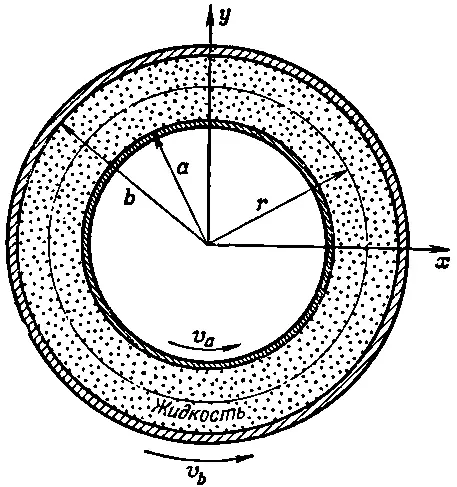
Фиг. 41.3. Поток жидкости между двумя концентрическими цилиндрами, вращающимися с разными угловыми скоростями.

Возникает вопрос, каково распределение скоростей между цилиндрами? Чтобы ответить на него, начнем с получения формулы для вязкого сдвига в жидкости на расстоянии r от оси. Из симметрии задачи можно предположить, что поток всегда тангенциален и что его величина зависит только от r; v = v ( r ). Если мы понаблюдаем за соринкой в воде, расположенной на расстоянии r от оси, то ее координаты как функции времени будут

где ω= v / r . При этом х - и y-компоненты скорости равны

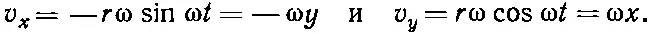(41.4)

Из формулы (41.3) получаем

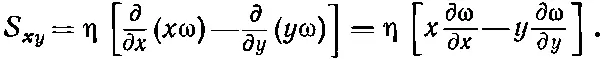(41.5)

Для точек с у =0 имеем ∂ω/∂ у =0, а х (∂ω/∂ х ) будет равно r( d ω/ dr ). Так что в этих точках

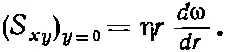(41.6)

(Разумно думать, что величина S должна зависеть от ∂ω/∂ r , когда ω не изменяется с r, жидкость находится в состоянии равномерного вращения и напряжения в ней не возникают.)

Вычисленное нами напряжение представляет собой тангенциальный сдвиг, одинаковый повсюду вокруг цилиндра. Мы можем получить момент сил , действующий на цилиндрической поверхности радиусом r, путем умножения напряжения сдвига на плечо импульса r и площадь 2π rl :

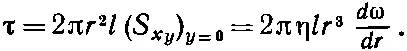(41.7)

Поскольку движение воды стационарно и угловое ускорение отсутствует, то полный момент, действующий на цилиндрическую поверхность воды между радиусами r и r+ dr , должен быть нулем; иначе говоря, момент сил на расстоянии r должен уравновешиваться равным ему и противоположно направленным моментом сил на расстоянии r+ dr , так что τ не должно зависеть от r. Другими словами, r 3(dω/dr) равно некоторой постоянной, скажем А , и

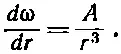(41.8)

Интегрируя, находим как ω изменяется с r:

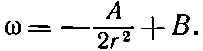(41.9)

Постоянные А и В должны определяться из условия, что ω=ω aв точке r = a , а ω=ω bв точке r = b . Тогда находим

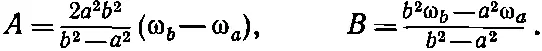(41.9)

Таким образом, ω как функция r нам известна, а стало быть, известно и v =ω r .

Если же нам нужно определить момент сил, то его можно получить из выражений (41.7) и (41.8):

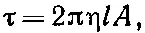
или

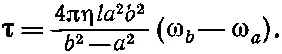(41.11)

Он пропорционален относительной угловой скорости двух цилиндров. Имеется стандартный прибор для измерения коэффициентов вязкости, который устроен следующим образом: один из цилиндров (скажем, внешний) посажен на ось, но удерживается в неподвижном состоянии пружинным динамометром, который измеряет действующий на него момент сил, а внутренний цилиндр вращается с постоянной угловой скоростью. Коэффициент вязкости определяется при этом из формулы (41.11).

Из определения коэффициента вязкости вы видите, что η измеряется в ньютон · сек / м 2. Для воды при 20° С

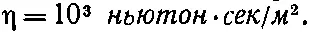
Часто удобнее бывает пользоваться удельной вязкостью , которая равна η, деленной на плотность ρ. При этом величины удельных вязкостей воды и воздуха сравнимы:

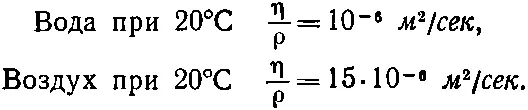(41.12)

Обычно вязкость очень сильно зависит от температуры. Например, для воды непосредственно над точкой замерзания отношение η/ρ в 1,8 больше, чем при 20° С.

Перейдем теперь к общей теории вязкого потока, по крайней мере настолько общей, насколько это и известно человеку. Вы уже понимаете, что компоненты сдвиговых напряжений сдвига пропорциональны пространственным производным от различных компонент скорости, таких, как ∂ v x /∂ y или ∂ v y /∂ х . Однако в общем случае сжимаемой жидкости в напряжениях есть и другой член, который зависит от других производных скорости. Общее выражение имеет вид

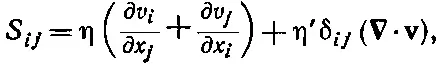(41.13)

где х i — какая-либо из координат х, у или z ; v i — какая-либо з прямоугольных составляющих скорости. (Значок δ ijобозначает символ Кронекера, который равен единице при i = j и нулю при i ≠ j .) Ко всем диагональным элементам S ij тензора напряжений прибавляется дополнительный член η' ∇· v. Если жидкость несжимаема, то ∇· v=0 и дополнительного члена не появляется, так что он действительно имеет отношение к внутренним силам при сжатии. Для описания жидкости, точно так же как и для описания однородного упругого тела, требуются две постоянные. Коэффициент η представляет «обычный» коэффициент вязкости, который мы уже учитывали. Он называется также первым коэффициентом вязкости , а новый коэффициент η' называется вторым коэффициентом вязкости .