Ричард Фейнман - Том 2. Электромагнетизм и материя

Подсчитаем сначала, сколько зарядов проходит через воображаемую плоскость, когда материал поляризуется. Количество заряда, проходящее через поверхность, есть просто Р , умноженное на площадь поверхности, если поляризация направлена по нормали к поверхности. Разумеется, если поляризация касательна к поверхности, то через нее не пройдет ни одного заряда.

Продолжая прежние рассуждения, легко понять, что количество заряда, прошедшее через любой элемент поверхности, пропорционально компоненте Р, перпендикулярной к поверхности. Сравним фиг. 10.6 и 10.5.

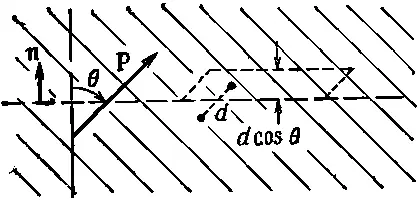
Фиг. 10.6. Количество ааряда, прошедшее через элемент воображаемой поверхности в диэлектрике, пропорционально компоненте Р, нормальной к поверхности.

Мы видим, что уравнение (10.5) в общем случае должно быть записано так:

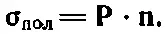(10.12)

Если мы имеем в виду воображаемый элемент поверхности внутри диэлектрика, то формула (10.12) дает заряд, который прошел через поверхность, но не приводит к результирующему поверхностному заряду, потому что возникают равные и противоположно направленные вклады от диэлектрика по обе стороны поверхности.

Однако смещение зарядов может привести к появлению объемной плотности зарядов. Полный заряд, выдвинутый из объема V за счет поляризации, есть интеграл от внешней нормальной составляющей Рпо поверхности S , охватывающей объем (фиг. 10.7).

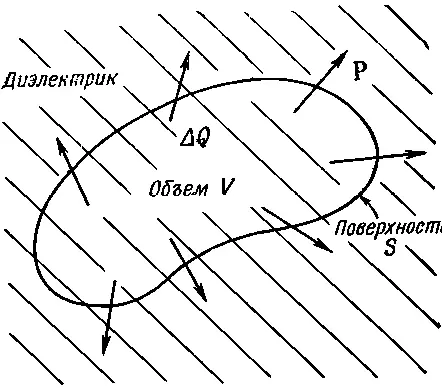
Фиг. 10.7. Неоднородная поляризация Р может приводить к появлению результирующего заряда внутри диэлектрика.

Такой же излишек зарядов противоположного знака остается внутри. Обозначая суммарный заряд внутри V через ΔQ пол, запишем

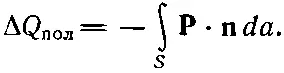(10.13)

Мы можем отнести ΔQ полза счет объемного распределения заряда с плотностью ρ пол, так что

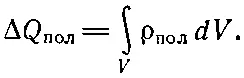(10.14)

Комбинируя оба уравнения, получаем

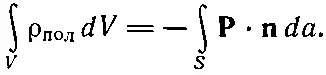(10.15)

Мы получили разновидность теоремы Гаусса, связывающую плотность заряда поляризованного материала с вектором поляризации Р. Мы видим, что она согласуется с результатом, полученным для поверхностного поляризационного заряда или же для диэлектрика в плоском конденсаторе. Уравнение (10.15) с гауссовой поверхностью S , изображенной на фиг. 10.1, дает в правой части интеграл по поверхности, равный Р ΔA, а в левой части заряд внутри объема оказывается σ полΔA, так что мы снова получаем σ= Р .

Точно так же, как мы делали в случае закона Гаусса для электростатики, мы можем перейти в уравнении (10.15) к дифференциальной форме, пользуясь математической теоремой Гаусса:

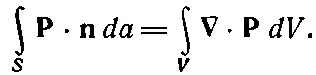
Мы получаем

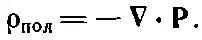(10.16)

Если поляризация неоднородна, ее дивергенция определяет появляющуюся в материале результирующую плотность зарядов. Подчеркнем, что это совсем настоящая плотность зарядов; мы называем ее «поляризационным зарядом», только чтобы помнить, откуда она взялась.

Давайте теперь свяжем полученные нами результаты с тем, что мы уже узнали в электростатике. Основное уравнение имеет вид

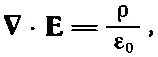(10.17)

где ρ — плотность всех электрических зарядов. Поскольку уследить за поляризационными зарядами непросто, удобно разбить ρ на две части. Обозначим снова через ρ ползаряды, появляющиеся за счет неоднородной поляризации, а остальную часть назовем ρ своб. Обычно ρ свобозначает заряд, сообщаемый проводникам или распределенный известным образом в пространстве. В этом случае уравнение (10.17) приобретает вид

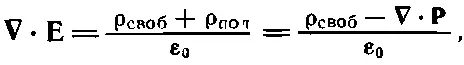
или

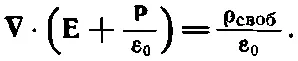(10.18)

Уравнение для ротора от Е , конечно, не меняется:

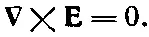(10.19)

Подставляя Риз уравнения (10.8), получаем более простое уравнение:

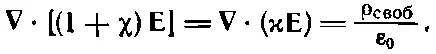(10.20)

Это и есть уравнения электростатики в присутствии диэлектриков. Они, конечно, не дают ничего нового, но имеют вид, более удобный для расчетов в тех случаях, когда ρ свобизвестно, а поляризация Рпропорциональна Е.

Заметьте, что мы не вытащили «константу» диэлектрической проницаемости ϰ за знак дивергенции. Это потому, что она может не быть всюду одинаковой. Если она повсюду одинакова, то ее можно выделить в качестве множителя и уравнения станут в точности обычными уравнениями электростатики, где только ρ свобнужно поделить на ϰ. В написанной нами форме уравнения годятся в общем случае, когда в разных местах поля расположены разные диэлектрики. В таких случаях решить уравнения иногда бывает очень трудно.

Здесь следует отметить один момент, имеющий историческое значение. На заре рождения электричества атомный механизм поляризации не был еще известен и о существовании ρ полне знали. Заряд ρ свобсчитался равным всей плотности зарядов. Чтобы придать уравнениям Максвелла простой вид, вводили новый вектор Dкак линейную комбинацию Еи Р:

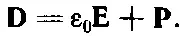(10.21)

В результате уравнения (10.18) и (10.19) записывались в очень простом виде:

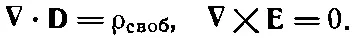(10.22)

Можно ли их решить? Только когда задано третье уравнение, связывающее Dи Е. Если справедливо уравнение (10.8), то эта связь есть