Ричард Фейнман - Том 2. Электромагнетизм и материя

Ответ заключается в поляризации диэлектрика, помещенного в электрическое поле. Возникают поляризационные заряды обоих знаков, притягиваемые и отталкиваемые расческой. Однако в результате получается притяжение, потому что поле поблизости от расчески сильнее, чем вдали от нее, ведь расческа не бесконечна. Ее заряд локализован. Нейтральный кусочек бумаги не притянется ни к одной из параллельных пластин конденсатора. Изменение поля составляет существенную часть механизма притяжения.

Как показано на фиг. 10.8, диэлектрик всегда стремится из области слабого поля в область, где поле сильнее.

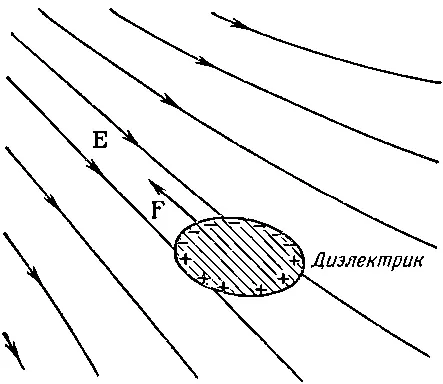
Фиг. 10.8. На диэлектрик в неоднородном поле действует сила, направленная в сторону областей с большей напряженностью поля.

В действительности можно показать, что сила, действующая на малые объекты, пропорциональна градиенту квадрата электрического поля. Почему она зависит от квадрата поля? Потому что индуцированные поляризационные заряды пропорциональны полям, а для данных зарядов силы пропорциональны полю. Однако, как мы уже указывали, результирующая сила возникает, только если квадрат поля меняется от точки к точке. Следовательно, сила пропорциональна градиенту квадрата поля. Константа пропорциональности включает помимо всего прочего еще диэлектрическую проницаемость данного тела и зависит также от размеров и формы тела.

Есть еще одна близкая задача, в которой сила, действующая на диэлектрик, может быть найдена точно. Если мы возьмем плоский конденсатор, в котором плитка диэлектрика задвинута лишь частично (фиг. 10.9), то возникнет сила, вдвигающая диэлектрик внутрь.

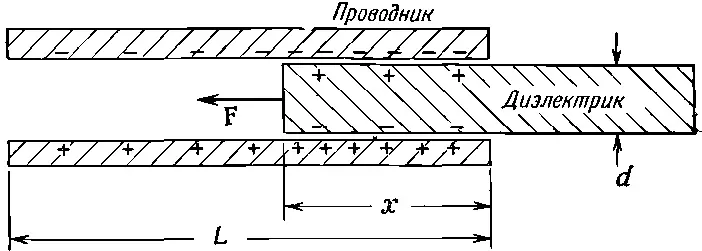
Фиг. 10.9. Сила, действующая на диэлектрик в плоском конденсаторе, может быть вычислена с помощью закона сохранения энергии.

Провести детальное исследование силы очень трудно; оно связано с неоднородностями поля вблизи концов диэлектрика и пластин. Однако если мы не интересуемся деталями, а просто используем закон сохранения энергии, то силу легко вычислить. Мы можем определить силу с помощью ранее выведенной формулы. Уравнение (10.28) эквивалентно такому:

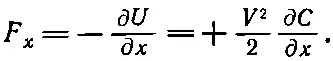(10.30)

Нам осталось только найти, как меняется емкость в зависимости от положения плитки диэлектрика.

Пусть полная длина пластин есть L, ширина их равна W , расстояние между пластинами и толщина диэлектрика равна d , а расстояние, на которое вдвинут диэлектрик, есть х . Емкость есть отношение полного свободного заряда на пластинах к разности потенциалов между пластинами. Выше мы видели, что при данном потенциале V поверхностная плотность свободных зарядов равна ϰε 0V/d. Следовательно, полный заряд пластин равен

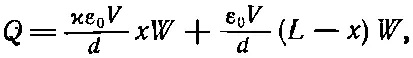
откуда мы находим емкость

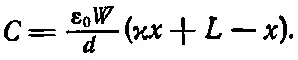(10.31)

С помощью (10.30) получаем

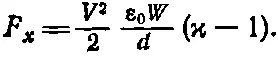(10.32)

Но пользы от этого выражения не очень много, разве только вам понадобится определить силу именно в таких условиях. Мы хотели лишь показать, что можно подчас избежать страшных осложнений при определении сил, действующих на диэлектрики, если пользоваться энергией, как это было в настоящем случае.

В нашем изложении теории диэлектриков мы имели дело только с электрическими явлениями, принимая как факт, что поляризация вещества пропорциональна электрическому полю. Почему возникает такая пропорциональность — вопрос, представляющий, пожалуй, еще больший интерес для физики. Стоит нам понять механизм возникновения диэлектрической проницаемости с атомной точки зрения, как мы сможем использовать измерения диэлектрической проницаемости в изменяющихся условиях для получения подробных сведений о строении атомов и молекул. Эти вопросы будут частично изложены в следующей главе.

Повторить : гл. 3 (вып. 3) «Как возникает показатель преломления»; гл. 40 (вып. 4) «Принципы статистической механики »

В этой главе мы поговорим о том, почему вещество бывает диэлектриком. В предыдущей главе мы указывали, что свойства электрических систем с диэлектриками можно было бы понять, предположив, что электрическое поле, действуя на диэлектрик, индуцирует в атомах дипольный момент. Именно, если электрическое поле Eиндуцирует средний дипольный момент в единице объема Р , то диэлектрическая проницаемость ϰ дается выражением

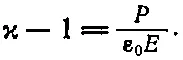(11.1)

О применениях этого выражения мы уже говорили; сейчас же нам нужно обсудить механизм возникновения поляризации внутри материала под действием электрического поля. Начнем с самого простого примера — поляризации газов. Но даже в газах возникают сложности: существуют два типа газов. Молекулы некоторых газов, например кислорода, в каждой молекуле которого имеются два симметричных атома, лишены собственного дипольного момента. Зато молекулы других газов, вроде водяного пара (у которого атомы водорода и кислорода образуют несимметричную молекулу), обладают постоянным электрическим дипольным моментом. Как мы отмечали в гл. 6 и 7, в молекуле водяного пара атомы водорода в среднем имеют положительный заряд, а атом кислорода — отрицательный. Поскольку центры тяжести положительного и отрицательного зарядов не совпадают, то распределение всего заряда в молекуле обладает дипольным моментом. Такая молекула называется полярной молекулой. А у кислорода вследствие симметрии молекулы центр тяжести и положительных, и отрицательных зарядов один и тот же, так что это неполярная молекула. Она, правда, может стать диполем, если ее поместить в электрическое поле. Формы этих двух типов молекул нарисованы на фиг. 11.1.

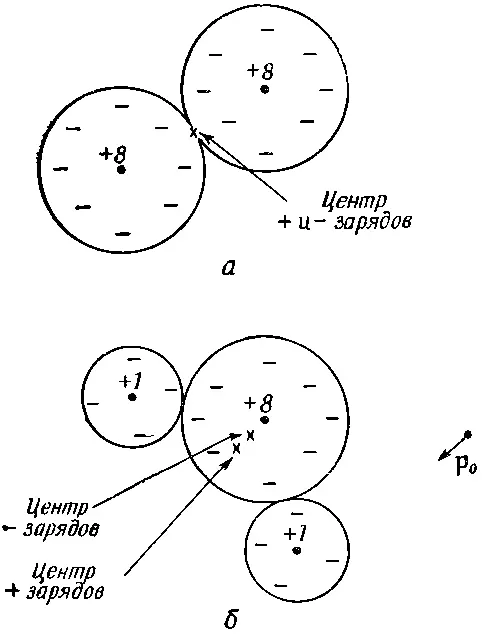
Фиг. 11.1. Молекула кислорода с нулевым дипольным моментом (а) и молекула воды с постоянным дипольным моментом р 0 (б).