Ричард Фейнман - Том 2. Электромагнетизм и материя

Займемся сначала поляризацией неполярных молекул. Начнем с простейшего случая одноатомного газа (например, гелия). Когда атом такого газа находится в электрическом поле, электроны его тянутся в одну сторону, а ядро — в другую, как показано на рис. 10.4. Хотя атомы имеют очень большую жесткость по отношению к электрическим силам, которые мы можем приложить к ним на опыте, центры зарядов чуть-чуть смещаются относительно друг друга и индуцируется дипольный момент. В слабых полях величина смещения, а следовательно, и дипольного момента пропорциональна напряженности электрического поля. Смещение электронного распределения, которое приводит к этому типу индуцированного дипольного момента, называется электронной поляризацией .

Мы уже обсуждали воздействие электрического поля на атом в гл. 31 (вып. 3), когда занимались теорией показателя преломления. Подумав немного, вы сообразите, что теперь нужно сделать то же, что и тогда. Только теперь нас заботят поля, не меняющиеся со временем, тогда как показатель преломления был связан с полями, зависящими от времени.

В гл. 31 (вып. 3) мы предполагали, что центр электронного заряда атома, помещенного в осциллирующее электрическое поле, подчиняется уравнению

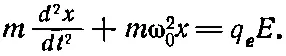(11.2)

Первый член — это произведение массы электрона на его ускорение, а второй — возвращающая сила; справа стоит сила, действующая со стороны внешнего электрического поля. Если электрическое поле меняется с частотой ω, то уравнение (11.2)

допускает решение

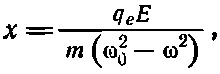(11.3)

имеющее резонанс при ω=ω 0. Когда раньше мы нашли это решение, то интерпретировали ω 0как частоту, при которой атом поглощает свет (она лежит либо в оптической, либо в ультрафиолетовой области, в зависимости от атома). Для нашей цели, однако, достаточно случая постоянных полей, т.е. ω=0; поэтому мы можем пренебречь членом с ускорением в (11.2) и получаем смещение

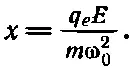(11.4)

Отсюда находим дипольный момент р одного атома

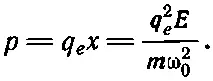(11.5)

В таком подходе дипольный момент р действительно пропорционален электрическому полю.

Обычно пишут

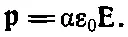(11.6)

(Снова ε 0вошло по историческим причинам.) Постоянная α называется поляризуемостью атома и имеет размерность L 3. Это мера того, насколько легко индуцировать электрическим полем дипольный момент у атома. Сравнивая (11.5) и (11.6), получаем, что в нашей простой теории

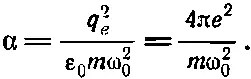(11.7)

Если в единице объема содержится N атомов, то поляризация (дипольный момент единицы объема) дается формулой

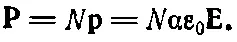(11.8)

Объединяя (11.1) и (11.8), получаем

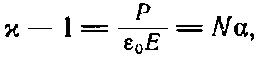(11.9)

или в силу (11.7)

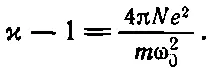(11.10)

С помощью уравнения (11.9) можно предсказать, что диэлектрическая проницаемость х различных газов должна зависеть от плотности газа и от резонансной частоты ω 0.

Наша формула, конечно, лишь очень грубое приближение, потому что в уравнении (11.2) мы воспользовались моделью, игнорирующей тонкости квантовой механики. Например, мы считали, что атом имеет только одну резонансную частоту, тогда как на самом деле их много. Чтобы по-настоящему вычислить поляризуемость атомов, нужно воспользоваться последовательной квантовомеханической теорией, однако и классический подход, изложенный выше, дает вполне разумную оценку.

Посмотрим, сможем ли мы получить правильный порядок величины диэлектрической проницаемости какого-нибудь вещества. Возьмем, к примеру, водород. Мы уже оценивали (вып. 4, гл. 38) энергию, необходимую для ионизации атома водорода, и получили приближенно

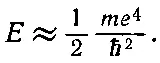(11.11)

Для оценки собственной частоты ω 0можно положить эту энергию равной ℏω 0— энергии атомного осциллятора с собственной частотой ω 0. Получаем

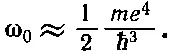
Пользуясь этой величиной в уравнении (11.7), находим электронную поляризуемость

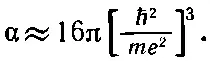(11.12)

Величина ( ℏ 2/ me 2) есть радиус основной орбиты атома Бора (см. вып. 4, гл. 38), равный 0,528 А. При нормальном давлении и температуре (1 атм , 0°С) в газе на 1 см 3приходится 2,69·10 19атомов, и уравнение (11.9) дает

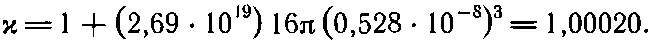(11.13)

Измеренная на опыте диэлектрическая проницаемость равна

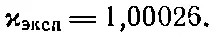
Видите, наша теория почти правильна. Лучшего нельзя было и ожидать, потому что измерения проводились, конечно, с обычным водородом, обладающим двухатомными молекулами, а не одиночными атомами. Не следует удивляться тому, что поляризация атомов в молекуле не совсем такая, как поляризация отдельных атомов. На самом деле молекулярный эффект не столь велик. Точное квантовомеханическое вычисление величины α для атомов водорода дает результат, превышающий (11.12) примерно на 12% (вместо 16πполучается 18π), поэтому он предсказывает для диэлектрической проницаемости значение, более близкое к наблюденному. Во всяком случае, совершенно очевидно, что наша модель диэлектрика вполне хороша.

Еще одна проверка нашей теории. Попробуем применить уравнение (11.12) к атомам с большей частотой возбуждения. Например, чтобы отобрать электрон у гелия, требуется 24,5 в , тогда как для ионизации водорода необходимы 13,5 в . Поэтому мы предположим, что частота поглощения ω 0для гелия должна быть примерно в два раза больше, чем для водорода, а α должна быть меньше в четыре раза. Мы ожидаем, что