Ричард Фейнман - Том 3. Квантовая механика

Теперь мы завершили все необходимые видоизменения наших основных уравнений, нужные для работы с континуумом базисных состояний, соответствующих точкам на прямой. Обобщение на три измерения вполне очевидно: во-первых, координата х заменяется вектором r; во-вторых, интегралы по х заменяются на интегралы по х, у и z (иными словами, они становятся интегралами по объему); в-третьих, одномерную δ-функцию надо заменить просто произведением трех δ-функций от x , от y и от z : δ( х - х ')δ( у - у ')δ( z - z '). Собирая все вместе, получаем следующую совокупность уравнений для амплитуд частицы в трехмерном мире:

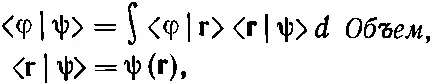(14.45)

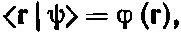(14.46)

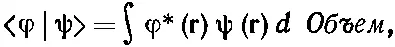(14.47)

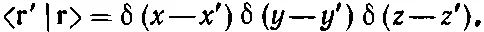(14.48)

А что бывает, когда частиц не одна, а больше? Мы расскажем вам, как управляться с двумя частицами, и вы сразу поймете, что нужно делать, если вам понадобится оперировать с несколькими частицами. Пусть имеются две частицы; назовем их № 1 и № 2. Что применить в качестве базисных состояний? Одну вполне приемлемую совокупность можно задать, сказав, что частица № 1 находится в х 1, а частица № 2 — в х 2, и записав это в виде | x 1, х 2>. Заметьте, что указание координаты только одной частицы не определяет базисного состояния. Каждое базисное состояние обязано определять условия всей системы целиком. Вы не должны думать, что каждая частица движется независимо как трехмерная волна. Всякое физическое состояние |ψ> можно определить, задав все амплитуды < x 1, х 2|ψ> того, что пара частиц будет обнаружена в х 1и x 2. Эта обобщенная амплитуда поэтому является функцией двух совокупностей координат x 1и x 2. Вы видите, что такая функция — это уже не волна в смысле колебания, которое разбегается в трех измерениях. Точно так же это и не простое произведение двух самостоятельных волн, по одной для каждой частицы. Это в общем случае какая-то волна в шести измерениях, определяемых числами х 1и x 2. Если в природе имеются две взаимодействующие частицы, то не существует способа описать то, что происходит с одной из частиц, попытавшись выписать волновую функцию для нее одной. Известные парадоксы, которые мы рассматривали в первых главах (где объявлялось, что измерения, проделанные над одной частицей, в состоянии предсказать, что будет с другой, или что они могут разрушить интерференцию), причинили людям много неприятностей, потому что они пытались придумывать волновую функцию одной отдельной частицы вместо правильной волновой функции координат обеих частиц. Полное описание можно правильно провести только в терминах функций координат обеих частиц.

До сих пор мы просто заботились о том, как бы записать состояния, которые бы учитывали, что электрон может находиться в пространстве где угодно. Теперь же следует позаботиться о включении в наше описание физики того, что может произойти в тех или иных обстоятельствах. Как и прежде, надо подумать о том, как состояния будут меняться со временем. Если у нас есть состояние |ψ>, которое несколько позже переходит в другое состояние |ψ>, то положение в любой момент мы сможем описать, сделав волновую функцию (т. е. попросту амплитуду < r|ψ>) функцией не только координат, но и времени. Частицу в данных условиях можно будет тогда описывать, задавая меняющуюся во времени волновую функцию ψ( r, t )=ψ( х, у, z, t ). Эта меняющаяся во времени волновая функция описывает эволюцию последовательных состояний, которая происходит с течением времени. Это так называемое «координатное представление»; оно дает проекции состояния |ψ> на базисные состояния | r> и не всегда может считаться самым удобным, но мы с него и начнем.

В гл. 6 мы описали на языке гамильтониана Н ij ., как состояния меняются во времени. Мы видели, что временная вариация различных амплитуд дается матричным уравнением

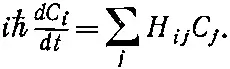(14.49)

Это уравнение говорит, что изменение во времени каждой из амплитуд С i пропорционально сумме всех прочих амплитуд С j с коэффициентами Н ij .

Как должно выглядеть (14.49) при континууме базисных состояний | x >? Вспомним сперва, что (14.49) можно также записать в виде

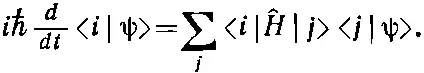
Теперь ясно, что делать. Для x -представления следует писать

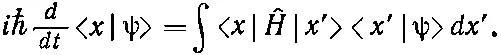(14.50)

Сумма по базисным состояниям | j > заменяется интегралом по х '. Поскольку < х |^ H | х '> должна быть какой-то функцией от x и х ', запишем ее как Н ( х, х '), что соответствует Н ij в (14.49). Тогда (14.50) это то же самое, что

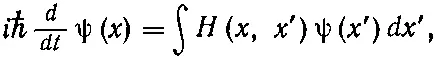(14.51)

где

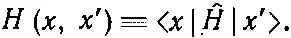
Согласно (14.51), быстрота изменения ψ в точке х зависела бы от значений ψ во всех других точках х '; множитель Н ( х, х ') — это амплитуда (в единицу времени) того, что электрон перепрыгнет из х ' в x . Оказывается, однако, что в природе эта амплитуда всюду, кроме точек х ', очень близких к х, равна нулю . Это означает, как мы видели на примере цепочки атомов в начале главы [см. (14.12)], что правая часть (14.51) может быть полностью выражена только через ψ и ее производные по x в точке х .

Для частицы, которая свободно движется в пространстве, не подвергаясь действию каких-либо сил и возмущений, правильный физический закон таков:

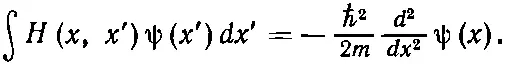
Откуда это получается? Это невозможно вывести из чего-либо нам уже известного. Это рождено в голове Шредингера, это выдумано им в битве за понимание экспериментальных наблюдений реального мира. Может быть, какой-то ключ к тому, почему так должно быть, вам дадут размышления по поводу нашего вывода уравнения (14.12), которое проистекло из рассмотрения распространения электрона в кристалле.