Ричард Фейнман - Том 3. Квантовая механика

Конечно, от свободных частиц проку мало. Что будет, если к частице приложить силы? Что ж, если действующая на частицу сила может быть описана с помощью скалярного потенциала V ( х ) (что означает, что речь идет не о магнитных силах, а об электрических) и если мы ограничимся низкими энергиями, чтобы иметь право пренебрегать теми сложностями, которые возникают при релятивистском движении, то гамильтониан, который укладывается в реальный мир, таков:

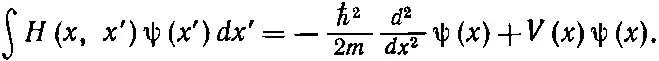(14.52)

Опять-таки некоторый ключ к происхождению этого уравнения вы получите, если вернетесь к движению электрона в кристалле и посмотрите, как надо изменить уравнения, если энергия электрона медленно меняется от атома к атому, как если бы к кристаллу было приложено электрическое поле. Тогда член Е 0в (14.7) будет медленно меняться в зависимости от места и будет соответствовать новому слагаемому, появившемуся в (14.52). [Вас может удивить, отчего мы сразу перешли от (14.51) к (14.52), а не дали правильного выражения для амплитуды Н ( х, х ')=< х |^ H | х '>. Да потому, что Н ( х, х ') можно написать только с помощью необычных алгебраических функций, а интеграл в правой части (14.51) выражается через привычные вещи. Если вам это в самом деле интересно, то вот смотрите: Н ( х, х ') можно записать так:

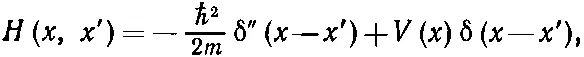
где δ'' означает вторую производную δ-функции. Эту довольно странную функцию можно заменить чуть более удобным и полностью ей равнозначным алгебраическим выражением

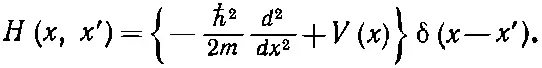
Мы не будем пользоваться этими формулами, а прямо будем работать с (14.52).]

Если теперь взять выражение (14.52) и подставить в (14.50) вместо интеграла, то для ψ( х )=< х |ψ> получится дифференциальное уравнение

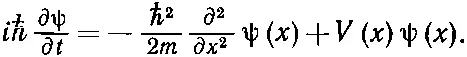(14.53)

Совершенно очевидно, что надлежит поставить вместо (14.53), если нас интересует трехмерное движение. Надо только d 2/ dx 2заменить на

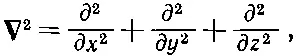
а V ( х ) заменить на V ( x, у, z ). Для электрона, движущегося в поле с потенциалом V ( х, у , z), амплитуда ψ( х, у, z ) удовлетворяет дифференциальному уравнению

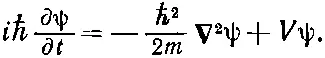(14.54)

Называется оно уравнением Шредингера и было первым известным квантовомеханическим уравнением. Его написал Шредингер, прежде чем было открыто любое другое описанное в этом томе уравнение.

Хотя мы здесь пришли к нему совсем иным путем, но появление этого уравнения в 1926 г., когда Шредингер впервые его написал, явилось великим историческим моментом, отметившим рождение квантовомеханического описания материи. Многие годы внутренняя атомная структура вещества была великой тайной. Никто не был в состоянии понять, что скрепляет вещество, отчего существует химическая связь, и, особенно, как атомам удается быть устойчивыми. Хотя Бор и смог дать описание внутреннего движения электрона в атоме водорода, которое, казалось бы, объясняло наблюдаемый спектр лучей, испускаемых этим атомом, но причина, отчего электроны движутся именно так, оставалась тайной. Шредингер, открыв истинные уравнения движения электронов в масштабах атома, снабдил нас теорией, которая позволила рассчитать атомные явления количественно, точно и подробно. В принципе его уравнение способно объяснить все атомные явления, кроме тех, которые связаны с магнетизмом и теорией относительности. Оно объясняет уровни энергии атома и все, что касается химической связи. Но, конечно, это объяснение только в принципе. Математика вскоре становится столь сложной, что точно решить удается только простейшие задачи. Одни лишь атомы водорода и гелия были рассчитаны с высокой точностью. Однако путем различных приближений, порой весьма сомнительных, можно многое понять и в более сложных атомах и в химической связи молекул. Некоторые из этих приближений были показаны в предыдущих главах.

Уравнение Шредингера в том виде, в каком мы его записали, не учитывает каких-либо магнитных эффектов. Их, правда, можно приближенно принять во внимание, добавив в уравнение еще другие члены. Но, как мы убедились раньше, магнетизм — это эффект существенно релятивистский, так что правильное описание движения электрона в произвольном электромагнитном поле можно обсуждать только в рамках надлежащего релятивистского уравнения. Правильное релятивистское уравнение для движения электрона было открыто Дираком через год после того, как Шредингер придумал свое уравнение; оно имеет совершенно другой вид. Мы его не успеем здесь изучить.

Прежде чем перейти к рассмотрению некоторых следствий из уравнения Шредингера, хотелось бы продемонстрировать, как оно выглядит для системы многих частиц. Мы не будем им пользоваться, а просто хотим показать вам его, чтобы подчеркнуть, что волновая функция ψ не просто обычная волна в пространстве, а функция многих переменных. Если частиц много, уравнение превращается в

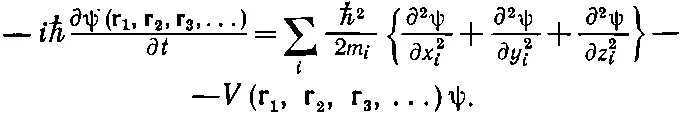(14.55)

Потенциальная функция V — это то, что классически соответствует полной потенциальной энергии всех частиц. Если на частицы не действуют внешние силы, то функция V есть попросту электростатическая энергия взаимодействия всех частиц. Иначе говоря, если заряд i -й частицы равен Z i q e , то функция V просто равна [57] Помните, еще раньше мы условились, что e 2 ≡ q e 2 /4πε 0

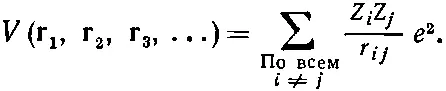(14.56)

В одной из последующих глав мы на каком-нибудь примере более подробно разберем решение уравнения Шредингера. А сейчас мы хотим показать вам, как получается одно из самых замечательных следствий из уравнения Шредингера — тот поразительный факт, что из дифференциального уравнения, в которое входят только непрерывные функции непрерывных пространственных переменных, могут возникнуть квантовые эффекты, как, например, дискретные уровни энергии в атоме. Нам надо понять следующий существенный факт: как это может быть, что энергия электрона, попавшего в потенциальный «колодец» и вынужденного оставаться в определенной области пространства, с необходимостью принимает значения только из точно определенной дискретной их совокупности.